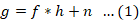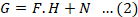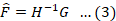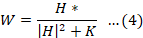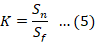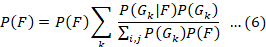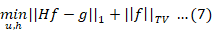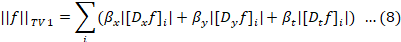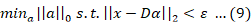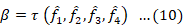Research Article

Fused Restoration Filtering for Single-Image Blind Deblurring

Aftab Khan*, Yasir Khan and Saleem Iqbal

Department of Computer Science (DCS), Allama Iqbal Open University (AIOU), Islamabad, 46000, Pakistan.

Received: October 05, 2023; Accepted: November 25, 2023; Published: December 27, 2023

*Correspondence: Aftab Khan, Department of Computer Science (DCS), Allama Iqbal Open University (AIOU), Islamabad, 46000, Pakistan; Email: [email protected]

Citation: Khan, A., Y. Khan and S. Iqbal. 2023. Fused restoration filtering for single-image blind deblurring. Journal of Engineering and Applied Sciences, 42: 38-48.

DOI: https://dx.doi.org/10.17582/journal.jeas/42.38.48

Keywords: Blind deconvolution, Blind estimation, Digital image restoration, Image deblurring, Image fusion, Multi-scale transform (MST), Sparse representation (SR)

Copyright: 2023 by the authors. Licensee ResearchersLinks Ltd, England, UK.

This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Introduction

The challenge of restoring images from blurriness is a common issue encountered when attempting to reconstruct images, and it remains a vibrant topic of exploration within the realm of image manipulation research. Likely sources contributing to this blurriness include disturbances in the atmosphere, loss of focus, and the movement discrepancy between the camera and the subject (Du et al., 2023; Fergus et al., 2006; Shan et al., 2008; Welk et al., 2015).

Assuming the blurriness exhibits a universal quality and remains consistent across translations, the process of observation can be conceptualized as:

Where; g is the observed picture, f is the original image, * represents the convolution operator, h represents the camera transform function and n represents the noise (additive or multiplicative) (Lai et al., 2023; Shi et al., 2015). In the frequency domain, Equation 1 can be reformulated as:

In the absence of noise, deblurring simplifies to inverse filtering as depicted by Equation 3.

From Equation 3, the restoration process can be inferred as an inverse problem. If the camera’s transform function also known as the Point Spread Function (PSF) is known, then the degraded image can easily be restored. Regrettably, in real scenarios, the PSF is unavailable, so the degraded image cannot be restored easily. Researchers aim at recovering the blurred images without PSF information or technically stated “blindly” referring to such a type of restoration being termed Blind Image Deblurring (BID).

Various blurs affect the image differently as follows:

Atmospheric Turbulence Blur/Gaussian Blur: In order to successfully eliminate atmospheric blur, algorithms must consider the haziness and light dispersion brought on by atmospheric disturbances.

Out of Focus Blur: Deblurring is the process of recovering details that have been lost as a result of incorrect focus settings or problems with lenses. Iterative blind deconvolution is one approach used to adjust to different degrees of focus loss.

Motion blur: Due to movement variances, complex motion blur necessitates deblurring algorithms that take into account the motion’s direction and intensity. These algorithms frequently make use of attention-based or convolutional neural network (CNN) techniques.

Additive or Multiplicative Noise: n in deblurring equations denotes noise, which makes the restoration process more difficult and requires optimization techniques and denoising techniques to be integrated into deblurring algorithms.

Various techniques and restoration filters have been developed to address the problem of blind image restoration. This collection of schemes ranges from the frequency domain to the spatial domain, concurrent or separate PSF estimation methods, parametric to non-parametric (Almeida and Almeida, 2010; Cho and Lee, 2009) schemes, frequency domain to time domain to name a few.

The Iterative Blind Deconvolution (IBD) (Philips, 2005; Sanghvi et al., 2022) is one such example. Other examples include the Maximum Likelihood (ML) method (Katsaggelos and Lay, 1991; Lagendijk et al., 1990), the Minimum Entropy (MED) method (Wiggins, 1978), the non-negativity and support- constraint recursive inverse filter (NAS-RIF) (Kundur and Hatzinakos, 1998) the Wavelet Deconvolution and Decomposition (Huang and Wang, 2017; Kerouh and Serir, 2015) the Simulated Annealing (SA) (Banham and Katsaggelos, 1997) the multi-channel blind deconvolution (Kopriva, 2007) and the Maximum A-Posteriori (MAP) (Haritopoulos et al., 2002; Reeves and Mersereau, 1992; Whyte et al., 2012). Recent advances in machine learning have led to the utilization of vision transformers, deep learning and image super-resolution techniques for deblurring as well (Ali et al., 2023; Alshammri et al., 2022; Zhang et al., 2000).

Computationally, wiener deblurring is not excessively complicated. Because it uses techniques like convolution and frequency domain analysis, it is appropriate for processing tasks that call for a reasonable amount of speed. Richardson-Lucy Deblurring, on the other hand, presents greater difficulties for computers. It uses an iterative process based on conditional probability; thus, it will take several tries to get reliable results. The computing effort is greatly increased by its repetitive nature. The complexity range of Total Variation (TV) Deblurring is moderate to high. It adds some complexity by using space-time minimization and an Augmented Lagrangian approach. Although it increases flexibility, the regularization parameter may decrease computing efficiency.

Zhang et al. (2000) and Chi et al. (2019) introduce a novel method for blind picture deblurring that utilizes Convolutional Neural Networks (CNNs). The study conducted by Li and Wang on attention-based blind motion deblurring highlights the effectiveness of attention processes in improving certain picture areas. This is especially useful when dealing with intricate motion blur patterns (Li et al., 2023). The optimization strategies to improve blind picture restoration filters are introduced by Chen et al.’s recent work on adaptive Wiener deblurring, which shows promising results in a variety of datasets (Chen et al., 2015).

This research work focuses on concerns including the requirement for human parameter tweaking in restoration filters, possible problems with different deblurring methods currently in use, and attaining high-quality outcomes for photos that are blurry both naturally and intentionally. This study introduces an innovative strategy to diminish the necessity for adjusting filter parameters through the utilization of the image amalgamation method showcased in section 3. The novel amalgamated refinement filtering strategy is outlined in section 4. The experimental configuration is detailed in section 5, showcasing the simulated outcomes for different image datasets. This encompasses the outcomes of rectifying blurriness for both fabricated and authentic indistinct images. Section 5 also provides discourse and evaluation, whereas Section 6 delivers final remarks. Section 2, on the other hand, outlines the challenge of fine-tuning the restoration filters.

Materials and Methods

Restoration filters such as Wiener filtering (Salehi et al., 2020), Richardson-Lucy (Braxmaier, 2004; Fish et al., 1995), regularization (Sa and Majhi, 2011), and Total Variation (TV) (Rudin and Osher, 1994) depend upon manual setting of their parameters to generate a deblurred image. An estimate of the blurring PSF is input to the filters, the number of iterations or Signal-to-Noise Ratio (SNR) is set for the filter. The values of the iterations, the SNR or the smoothening parameter is set to produce the deblurred image with reduced ringing artefacts or speckles.

For the Wiener Filter given by Equation 4, the effect of the Noise-to-Signal (NSR) term, depicted by K, on the deblurred image is very significant.

Here, |H|2 is the power spectrum of the blurring kernel, and Sn and Sf present the noise power and original image power, respectively. Within the context of Wiener filtering, achieving the most effective outcome involves adapting the Noise-to-Signal Ratio (NSR) element, denoted as K, for optimization. When K assumes a diminutive value, the resultant image exhibits sharpness but is prone to substantial noise. Conversely, if K takes on a larger value approaching 1, the image assumes a smoother appearance; however, the residual blurriness persists.

The Richardson-Lucy algorithm is an IBD scheme based on conditional probability. Mathematically, it can be expressed as follows:

In Equation 6, F shows the original image (the image that is to be restored), G is the degraded image (observed image), and k is the number of iterations. P(F) and P (G) representing the likelihoods of the initial image and the obscured image, correspondingly. The quantity of iterations can result in an amplification of noise within the rejuvenated image. Therefore, the variable k is adjusted to achieve the ideal count of iterations, thereby yielding the most optimal revitalized image.

TV algorithm is based on the Augmented Lagrangian (AL) method, in which AL is extended to space-time minimization. TV regularization functions are explored in space-time minimization.

This is called TV/L1 minimization, here H is the PSF, g is the degradation image, and µ is the regularization parameter. TV-norm ||f||TV is the anisotropic TV norm and can be expressed as:

In this context, Dx, Dy, and Dt stand for the progressive finite-difference operators along the horizontal, vertical, and time-related orientations. For TV deconvolution using MATLAB, the designated function is deconvtv (g, H, m, opts). Within this TV operation, m assumes the role of a regularization factor, intertwining the compromise between the Least Square Error (LSE) and the Television (TV) penalty. Larger values of m lean towards generating crisper outcomes, albeit with the drawback of potential noise amplification. On the contrary, smaller m values yield less noisy results, but the image may incur a smoother appearance. Determining the optimal m requires resolution during the minimization process (Chan et al., 2011; Lienhard et al., 2022).

To optimize the output quality, it’s imperative to manually fine-tune the parameters for these rejuvenation techniques. This entails assessing the interim deblurred output visually, followed by the appropriate modification of filter parameters. This procedure becomes even more intricate when the pursuit of an ideal parameter value is factored in, adding an extra layer of complexity.

As for the Wiener filter, which does the deblurring utilising four different Noise-to-Signal Ratio (NSR) values, the following sections will discuss the rationale for selecting these NSR values and elucidate their significance in achieving the best possible deblurring outcomes. Similarly, for the Richardson-Lucy method, for which iterations are very important, a thorough analysis of the rationale for the chosen iteration numbers will be presented. This additional explanation aims to promote transparency and methodological soundness in the restoration technique by giving readers a deeper knowledge of the decision-making process involved in parameter selection.

Within the scope of this investigation, image fusion emerges as a means to alleviate this workload and introduce automation into the deblurring process. The research employs the Multi-Scale Transform and Sparse Representation (MSTSR) fusion approach, a methodology expounded upon in the subsequent section.

Multi-scale transforms sparse representation (MSTSR) image fusion

The method of image fusion pertains to the amalgamation of two or more distinct images into a solitary composition with the aim of crafting a superior visual outcome. Within this current research draft, the Multi-Scale Transform Sparse Representation (MSTSR) methodology for image fusion takes center stage. This approach draws its foundation from the principles of Sparse Representation (SR) and Multi-Scale Transform (MST). In the MSTSR technique, the input imagery is systematically disassembled into low-frequency and high-frequency components through the application of a specified MST mechanism. Subsequently, the low-frequency components of the input images are seamlessly integrated, mirroring a similar process for the high-frequency bands. As a culminating step, the inverse Multi-Scale Transform is employed to meticulously rebuild the ultimate fused image by combining the modified low-frequency and high-frequency bands.

This process is illustrated in Figure 1.

 

This scheme demonstrates robustness in terms of providing high-quality fused images, particularly for multi-modal images. In this BID research, the multi-modal MSTSR scheme is able to merge these deblurred instances effectively by utilizing MST and SR approach of Liu et al. (2015) compared to other schemes which only use MST or SR approach. It is pertinent to mention that high-quality fusion results of MSTSR depend on the transform utilized by MST. The performance of the MSTSR fusion method may vary depending on the composition of the input photos. Pictures with rich details, complicated architecture, or erratic patterns could be difficult for the fusion algorithm to process. In these situations, the algorithm may find it difficult to integrate the high-frequency and low-frequency components, which could result in less-than-ideal outcomes.

The research work capitalizes on the merits of Multi-Scale Transform and Sparse Representation (MSTSR) image fusion, chosen for its competence in yielding a superior amalgamated image.

The use of Multi-Scale Transform Sparse Representation (MSTSR) for picture restoration is justified by its special advantages in blind deblurring scenarios. MSTSR excels in multi-scale information retention, offering a comprehensive representation of small elements that other fusion approaches sometimes overlook. Its ability to express sparsely makes it capable of accurately modeling complex patterns by enabling it to handle intricate details in hazy images with ease. The effectiveness of MSTSR has been demonstrated in earlier studies, and its adaptability to multi-modal images and effective integration of low- and high-frequency components further bolster its usefulness. In conclusion, MSTSR offers a comprehensive and proven approach to address the challenges associated with blind picture deblurring, thanks to its unique benefits.

In the subsequent section, an introduction is made to the MSTSR fusion technique adopted within this research endeavor. The foundations of MSTSR rest upon the principles of Sparse Representation (SR) and Multi-Scale Transform (MST). A brief overview of these two methodologies precedes the elucidation of the MSTSR algorithm.

Sparse representation (SR)

The fundamental assumption of SR can be stated as follows: “A signal x ∈ Rn can be approximately represented by a linear combination of a “few” atoms from a redundant dictionary D ∈ Rn*m (n < m), where n is the signal dimension, and m is the dictionary size. That is, the signal x can be expressed as x ≈ Dα, where α∈Rm is the unknown sparse coefficient vector. As the dictionary is over-complete, there are plentiful feasible explanations for this under-determined system of equations. The goal of SR is to compute the sparsest α which comprises the scarcest non-zero entries among all feasible solutions (Liu et al., 2015).

Mathematically, the sparset α can be obtained with the following sparse model:

Here ε > 0 is an error tolerance and ||a||0 denotes the l0-norm which counts the number of non-zero entries.

Multi-scale transform (MST)

The MST-based fusion methods consist of three steps: Decomposition, transformation, and reconstruction (Li et al., 2023). Firstly, the source images are decomposed into a multi-scale transform domain. Then the transformed coefficients are merged using a given fusion rule. Finally, the fused image is reconstructed by performing the corresponding inverse transform over the merged coefficients.

The MST-SR based image fusion approach entails the following four processes (Liu et al., 2015).

Step 1: MST decomposition

The image is split into low-pass and high-pass bands by utilizing a specific MST on two or more input images.

Step 2: Low-pass fusion

A sliding window technique is used to divide the low-pass bands into patches of size. Then these patches are rearranged into column vectors, and the mean values for each vector are normalized to zero to get vector. Using Orthogonal Matching Pursuit (OMP) algorithm, calculate the sparse coefficient vectors. Merge the sparse coefficient vectors (Mallat and Zhang, 1993) to get the final sparse vector by the popular “max-L1” rule. Repeat the above process for all the images’ patches to get all the fused vectors, reshape them into a pitch, and place them into their original position. As patches are overlapped, each pixel’s value in the final fused image is averaged over its accumulation times.

Step 3: High-pass fusion

In this step, the high-pass bands of the images are fused together with the famous “-max-absolute” rule using the absolute value of each coefficient as the activity level measurement. Then, apply the consistency verification scheme to ensure that a fused coefficient does not originate from a different source image from most of its neighbours. This can be implemented via a small majority filter.

Step 4: MST reconstruction

The final fused image fF is reconstructed by taking inverse MST over the final fused lower-pass bands and high-pass bands (Liu et al., 2015).

The fused restoration filtering approach for BID is presented in the section that follows.

Proposed image fusion based restoration filtering

Let τ represents the fusion algorithm, (F ̂n) represents the set of deblurred image estimates for the deblurred instances, filter parameters values given by R, then the fused deblurred image f ̂ can be given by Equation 10 as:

In the case of Wiener filter, R=[1e-02,8e-03,6e-03,4e-04] represent the four NSR values. For the Richardson-Lucy restoration, R= [8, 9, 10, 11] depict the four different iterations while R=[2, 3, 4, 5] represent the four regularization values for the TV deconvolution filter. The blurred image is deblurred four times for the different values of R for the corresponding filter. Then the recovered images are fused together by using MSTSR fusion technique to get final resultant recovered image. Through image fusion the recovered image achieves good perceptual as well as objective quality. The proposed algorithm is based on the fusion of various deblurring outputs in order to generate a high quality deblurred image independent of the manual tuning of classical restoration filters.

Figure 2 shows the overview of the fused restoration filter algorithm. The blurred image g is provided to the restoration filter, which estimates the deblurred images [f ̂1,f ̂2.......f ̂n] using the multiple parameter values given by the set R. These multiple estimates are then joined together using the MSTSR fusion algorithm to generate the single high-quality deblurred image.

 

Figure 3 shows the process of deblurring through fused restoration for the Lena image. Figure 3a shows the original image, while its corresponding blurred image is given in Figure 3b. Figure 3c-f are deblurred estimates using the Wiener filter for NSR values 1e-03, 8e-03, 6e-03, and 4e-04, respectively. A smaller NSR produces a sharper image as given in Figure 3f but at the cost of higher deblurring noise. High NSR values produce smooth images with relatively low noise but with a fair amount of residual blur still inherent in the deblurred image. Combining all four images of Figure 3c-f through the MSTSR algorithm produces a fused image containing sharp details as well as reduced noise. Figure 2a was blurred using a Gaussian blur of variance, σ2= 1.5.

 

Figure 4a and b show the deblurring quality computed by BRISQUE (Blind/Reference-less Image Spatial Quality Evaluator) (Mittal et al., 2012) and PSNR respectively for the deblurred image using four NSR values. Since the true variance is unknown, deblurring estimates the value over a range of variance σ2 from 0.1 to 5. BRISQUE computes image quality scores on a scale of 0 to 100. A smaller score of the BRISQUE measure depicts a high-quality image. PSNR, on the other hand, is measured in decibels (dB) and a high value depicts a high-quality image. It can be seen that the best estimates of variance are produced for the fused images. The NSR score of 4e-03 relates well with the BRISQUE scores values. But the fused image as seen in Figure 4f has better quality as compared to Figure 4e.

 

Figure 4b shows the PSNR values which confirm the effectiveness of the proposed fusion-based restoration filter. In the case of real blurred only BRISQUE scores were calculated as we have no reference image. PSNR is a full-reference quality measure and thus cannot be used in blind deconvolution but BRISQUE being a reference-less image quality measure can be utilized for blur estimation in blind deconvolution.

Results and Discussion

The simulations in the case of artificially blurred images included images blurred using the f special function in MATLAB. Simulations included the restoration of images under Gaussian, motion, and out-of-focus blur. Real blurred images captured by the first author were also used. To gauge the quality of the restoration techniques, the full reference PSNR and blind image quality measure BRISQUE have been utilized. The following section presents and analyses the results for artificially blurred images using fused restoration.

Deblurring artificially blurred images

Figure 5 shows the deblurring results for the Monarch image under the influence of Gaussian blur. Figure 4a shows the blurred image, while Figure 5b-d are the fused restorations using Wiener, Richardson-Lucy, and TV filtering, respectively. The fused Wiener filter reveals the best result as compared to the fused Richardson-Lucy and fused TV filter.

 

 

The fused Richardson-Lucy results inherit residual blur, while the TV filter produces a water-color effect. Results in Table 1 show a high value of PSNR and a low value of BRISQUE for the fused Wiener filter as compared to the other filters; thus, confirming the efficiency of the Wiener filter in terms of producing

 

Table 1: PSNR and BRISQUE values for the fused restoration filters in the case of artificial Gaussian, motion and out-of-focus blur.

Blur type	Fused / Non-fused restoration	Weiner		Richardson lucy		Total variation
		PSNR (dB)	BRISQUE	PSNR (dB)	BRISQUE	PSNR (dB)	BRISQUE
Gaussian blur	w1	29.9	34.8	27	38.7	30.4	39.4
	w2	30.1	34.2	27	37.9	30.4	38.9
	w3	30.3	33.4	27	37.5	30.4	39.3
	w4	31.4	32.5	27	37.5	30.4	39.8
	fused	31.2	32.5	27	36.6	30.4	39.1
Motion blur	w1	30.9	42.4	29.7	46.2	30.5	32.9
	w2	31	41.5	29.7	44.8	30.5	34.3
	w3	31.1	40	29.7	43.3	30.5	33.1
	w4	31.4	38.6	29.7	42.5	30.5	34
	fused	31.2	38.8	29.7	43.3	30.4	33.3
Out of focus Blur	w1	30	48.8	28.7	53.7	29.8	43.8
	w2	30.1	48.3	28.7	53.7	29.8	44.2
	w3	30.2	47	28.7	53.5	29.8	44.6
	w4	30.8	45.1	28.7	53	29.8	43.7
	fused	30.7	45.5	28.7	53.1	29.8	43.7

 

a high-quality image. The deblurred images using Wiener filter are 8 percent better as compared to the Richardson-Lucy filter and 3 percent more effective in comparison to TV deblurring.

 

Results in Figure 6 and 7 are achieved in the case of motion and out-of-focus deblurring. In Figure 6b and 7b, the results of fused Wiener filter are high quality as compared to the other restoration filters. PSNR and BRISQUE values corroborate this fact.

 

Deblurring real blurred images

Figure 8 shows the deblurring results in the case of real motion blur. This image was extracted from a video frame recorded under the camera by moving a label. The digits in the top level appear to recover well particularly in the case of the fused Richardson-Lucy filter as compared to the fused Wiener and fused TV filter. However, the small size digits at the bottom of

 

the image do not seem to recover using any of the fused filters. A possible reason could be that the text size is too small and the PSF is large which highly corrupts the text beyond recovery. In the case of real images, only BRISQUE scores can be calculated as the reference pristine image is not available. Table 2 shows the BRISQUE scores for Figures 8, 9 and 10. A low score is achieved in the case of the Richardson-Lucy filter depicting a high-quality image. w1, w2, w3, and w4 are the four deblurred images by trying four different values for the parameter of the restoration filters.

 

 

Table 2: BRISQUE values for the fused restoration filters in the case of real blurred image.

Image No.	Fusion data	Weiner	Richardson lucy	Total variation
Fig. 8	w1, w2	40.69, 34.80	40.69, 23.27	40.69, 54.74
	w3, w4	33.72, 32.93	21.18, 20.53	54.16, 53.28
	Fused	32.19	19.54	53.82
Fig. 9	w1, w2	49.07, 37.90	49.07, 25.84	49.07, 24.78
	w3, w4	37.70, 35.24	25.21, 21.93	29.32, 27.06
	Fused	34.87	22.91	26.52
Fig. 10	w1, w2	49.67, 48.26	49.67, 50.09	49.67, 55.38
	w3, w4	45.80, 46.76	48.09, 47.96	50.50, 49.87
	Fused	46.92	45.69	49.06

 

Conclusions and Recommendations

In this research work, image fusion was utilized to produce high-quality images in BID. The MSTSR fusion embedded in the restoration filters significantly increased the performance of the filtering in terms of the deblurred image quality. Among the Wiener Filter, Richardson Lucy, and TV deconvolution, the fused restoration demonstrated improved quality in terms of PSNR and BRISQUE values. This research has successfully reduced the hurdle of trying different parameters for blind deblurring filters. Results on artificial and real blurred images demonstrate the efficacy of utilizing image fusion for blind image restoration. The findings suggest the effectiveness of the image fusion process in aiding the blind deblurring process. The Wiener filter produces the best result for artificially blurred images, while the Richardson-Lucy filter succeeds in the case of real blurred images. Fusion methods, in general, may introduce artifacts in the deblurred image, especially when combining information from multiple sources. The MSTSR approach might be prone to generating artifacts, such as halos or ringing effects, particularly in regions with abrupt intensity changes or high-frequency details. This is envisioned to be addressed in the culminating research work.

Novelty Statement

This research work purposefully employs image fusion to eliminate the need for adjusting parameters for image deblurring filters

Author’s Contribution

Aftab Khan: Conceptualization, design, manuscript drafting, reviewing, and figure design.

Yasir Khan: Experimentation, data processing, and analysis.

Saleem Iqbal: Data processing, analysis, manuscript drafting, reviewing, and figure design.

Conflict of interest

The authors have declared no conflict of interest.

References

Ali, A.M., Benjdira, B., Koubaa, A., El-Shafai, W., Khan, Z. and Boulila, W.J.S., 2023. Vision transformers in image restoration: A survey. Sensors, 23(5): 2385. https://doi.org/10.3390/s23052385

Almeida, M.S.C. and Almeida, L.B., 2010. Blind and semi-blind deblurring of natural images. IEEE Trans. Image Proc., 19(1): 36-52. https://doi.org/10.1109/TIP.2009.2031231

Alshammri, G.H., Samha, A.K., El-Shafai, W., Elsheikh, E.A., Hamid, E.A., Abdo, M.I. and Abd El-Samie, F.E.J.I.A., 2022. Three-dimensional video super-resolution reconstruction scheme based on histogram matching and recursive Bayesian algorithms. IEEE Access., 10: 41935-41951. https://doi.org/10.1109/ACCESS.2022.3153409

Banham, M.R. and Katsaggelos, A.K., 1997. Digital Image Restoration. IEEE Signal Proc. Mag., 14(2): 24-41. https://doi.org/10.1109/79.581363

Braxmaier, C., 2004. Proceedings of the society of photo-optical instrumentation engineers (SPIE).

Chan, S.H., Khoshabeh, R., Gibson, K.B., Gill, P.E. and Nguyen, T.Q., 2011. An augmented lagrangian method for total variation video restoration. IEEE Trans. Image Proc., 20(11): 3097-3111. https://doi.org/10.1109/TIP.2011.2158229

Chen, H., Wang, C., Song, Y. and Li, Z., 2015. Split bregmanized anisotropic total variation model for image deblurring. J. Visual Commun. Image Represent., 31: 282-293. https://doi.org/10.1016/j.jvcir.2015.07.004

Chi, Z., Shu, X. and Wu, X., 2019. Joint demosaicking and blind deblurring using deep convolutional neural network. Paper presented at the 2019 IEEE international conference on image processing (ICIP). https://doi.org/10.1109/ICIP.2019.8803201

Cho, S. and Lee, S., 2009. Fast motion deblurring. ACM Trans. Graph., 28(5). https://doi.org/10.1145/1618452.1618491

Du, Y., Wu, H. and Cava, D.G., 2023. A motion-blurred restoration method for surface damage detection of wind turbine blades. Measurement, 217: 113031. https://doi.org/10.1016/j.measurement.2023.113031

Fergus, R., Singh, B., Hertzmann, A., Roweis, S.T. and Freeman, W.T., 2006. Removing camera shake from a single photograph. ACM Trans. Graph., 25(3): 787-794. https://doi.org/10.1145/1141911.1141956

Fish, D., Brinicombe, A., Pike, E. and Walker, J.J.J.A., 1995. Blind deconvolution by means of the Richardson–Lucy algorithm. J. Optic. Soc. Am. A, 12(1): 58-65. https://doi.org/10.1364/JOSAA.12.000058

Haritopoulos, M., Yin, H.J. and Allinson, N.M., 2002. Image denoising using self-organizing map-based nonlinear independent component analysis. Paper presented at the neural networks. https://doi.org/10.1016/S0893-6080(02)00081-3

Huang, H. and Wang, K., 2017. Texture-preserving deconvolution via image decomposition. Signal, image and video processing. https://doi.org/10.1007/s11760-017-1074-y

Katsaggelos, A.K. and Lay, K.T., 1991. Maximum-likelihood blur identification and image-restoration using the EM algorithm. IEEE Trans. Signal Proc., 39(3): 729-733. https://doi.org/10.1109/78.80894

Kerouh, F. and Serir, A., 2015. Wavelet-based blind blur reduction. Signal, Image Video Proc., 9(7): 1587-1599. https://doi.org/10.1007/s11760-014-0613-z

Kopriva, I., 2007. Approach to blind image deconvolution by multiscale subband decomposition and independent component analysis. J. Optic. Soc. Am. Optic. Image Sci. Vis., 24(4): 973-983. https://doi.org/10.1364/JOSAA.24.000973

Kundur, D. and Hatzinakos, D., 1998. A novel blind deconvolution scheme for image restoration using recursive filtering. IEEE Trans. Signal Proc., 46(2): 375-390. https://doi.org/10.1109/78.655423

Lagendijk, R.L., Tekalp, A.M. and Biemond, J., 1990. Maximum-likelihood image and blur identification. A unifying approach. Optic. Eng., 29(5): 422-435. https://doi.org/10.1117/12.55611

Lai, J., Xiong, J. and Shu, Z., 2023. Model-free optimal control of discrete-time systems with additive and multiplicative noises. Automatica, 147: 110685. https://doi.org/10.1016/j.automatica.2022.110685

Li, J., Wang, W., Nan, Y. and Ji, H., 2023. Self-supervised blind motion deblurring with deep expectation maximization. Paper presented at the 2023 IEEE/CVF conference on computer vision and pattern recognition (CVPR). https://doi.org/10.1109/CVPR52729.2023.01344

Li, Q., Wang, W. and Yan, S., 2023. Medical image fusion based on multi-scale transform and sparse representation. Paper presented at the fourteenth international conference on graphics and image processing (ICGIP 2022). https://doi.org/10.1117/12.2680002

Lienhard, F., Mortier, A., Buchhave, L., Collier C.A., López-Morales, M., Sozzetti, A. and Cosentino, R., 2022. Multi-mask least-squares deconvolution: Extracting RVs using tailored masks. Monthly Notices R. Astron. Soc., 513(4): 5328-5343. https://doi.org/10.1093/mnras/stac1098

Liu, Y., Liu, S. and Wang, Z., 2015. A general framework for image fusion based on multi-scale transform and sparse representation. Inf. Fusion, 24: 147-164. https://doi.org/10.1016/j.inffus.2014.09.004

Mallat, S.G. and Zhang, Z., 1993. Matching pursuits with time-frequency dictionaries. Signal Proc. IEEE Trans., 41(12): 3397-3415. https://doi.org/10.1109/78.258082

Mittal, A., Moorthy, A.K. and Bovik, A.C., 2012. No-reference image quality assessment in the spatial domain. IEEE Trans. Image Proc., 21(12): 4695-4708. https://doi.org/10.1109/TIP.2012.2214050

Philips, T., 2005. The mathematical uncertainty principle. Retrieved from http://www.ams.org/samplings/feature-column/fcarc-uncertainty

Reeves, S.J. and Mersereau, R.M., 1992. Blur identification by the method of generalized cross-validation. IEEE Trans. Image Proc., 1(3): 301-311. https://doi.org/10.1109/83.148604

Rudin, L.I. and Osher, S., 1994. Total variation based image restoration with free local constraints. Paper presented at the Proceedings of 1st international conference on image processing. https://doi.org/10.1109/ICIIP.2011.6108952

Sa, P.K. and Majhi, B., 2011. Adaptive edge preserving regularized image restoration. Paper presented at the 2011 International Conference on Image Information Processing.

Salehi, H., Vahidi, J., Abdeljawad, T., Khan, A. and Rad, S.Y.B.J.R.S., 2020. A SAR image despeckling method based on an extended adaptive wiener filter and extended guided filter. Remote Sens., 12(15): 2371. https://doi.org/10.3390/rs12152371

Sanghvi, Y., Gnanasambandam, A., Mao, Z. and Chan, S.H., 2022. Photon-limited blind deconvolution using unsupervised iterative kernel estimation. IEEE Trans. Comput. Imag., 8: 1051-1062. https://doi.org/10.1109/TCI.2022.3226947

Shan, Q., Jia, J. and Agarwala, A., 2008. High-quality motion deblurring from a single image. ACM Trans. Graph., 27(3): 10. https://doi.org/10.1145/1360612.1360672

Shi, Y., Chang, Q. and Yang, X., 2015. A robust and fast combination algorithm for deblurring and denoising. Signal, Image Video Proc., 9(4): 865-874. https://doi.org/10.1007/s11760-013-0513-7

Welk, M., Raudaschl, P., Schwarzbauer, T., Erler, M. and Läuter, M., 2015. Fast and robust linear motion deblurring. Signal, Image Video Proc., 9(5): 1221-1234. https://doi.org/10.1007/s11760-013-0563-x

Whyte, O., Sivic, J., Zisserman, A. and Ponce, J., 2012. Non-uniform deblurring for shaken images. Int. J. Comp. Vis., 98(2): 168-186. https://doi.org/10.1007/s11263-011-0502-7

Wiggins, R.A., 1978. Minimum entropy deconvolution. Geoexploration, 16(1-2): 21-35. https://doi.org/10.1016/0016-7142(78)90005-4

Zhang, Q.F., Yin, H.J. and Allinson, N.M., 2000. A simplified ICA based denoising method. In: Proceedings of the IEEE-INNS-ENNS international joint conference on neural networks, Los Alamitos: IEEE Computer Soc., V: 479-482.