Research Article

Analysis of Technical Efficiency of Sugarcane Crop in Khyber Pakhtunkhwa: A Stochastic Frontier Approach

Amjad Ali* and Abbas Ullah Jan

Department of Agricultural and Applied Economics, The University of Agriculture, Peshawar, Khyber Pakhtunkhwa, Pakistan.

Received | September 21, 2016; Accepted | January 22, 2017; Published | February 28, 2017

*Correspondence | Amjad Ali, Department of Agricultural and Applied Economics, The University of Agriculture, Peshawar; Email: [email protected]

Citation | Ali, A. and A.U. Jan. 2017. Analysis of technical efficiency of sugarcane crop in Khyber Pakhtunkhwa: A stochastic frontier approach. Sarhad Journal of Agriculture. 33(1): 69-79.

DOI | http://dx.doi.org/10.17582/journal.sja/2017.33.1.69.79

Keywords | Sugarcane, Technical efficiency, Stochastic Frontier Approach (SFA), Cobb Douglas (CD) production function, Khyber Pakhtunkha

Introduction

Sugarcane is the world largest crop by quantity, mainly grown for sugar and its by-product. Sugarcane production at world level increases from 1264.52 million tons to 2165.21 million tonnes during 2001-2013 showing significant increase. Brazil is the major sugarcane producer in world with total production of 768.09 million tons followed by India (341.20), China (128.63), Thailand (101.09), Pakistan (64.75), Mexico (61.38), Colombia (34.97), Indonesia (33.71), Philippines (31.77) and USA (28.91) (FAO, 2014).

Sugarcane is a major crop and play major role in economic wellbeing of the farming community of the country (Ahmad et al., 1991; Rehman et al., 1992). In Pakistan sugarcane crop is extensively planted in Sindh, Punjab and Khyber Pakhtunkhwa provinces. In 2014-15 it was grown on an area of 1141 thousand hectares with production of 62.652 million tonnes. Sugar industry depends upon cane cultivation. Sugarcane not only provides sugar but also provide bio fuel, fiber, organic fertilizer, chipboard, paper, molasses and ethanol as byproducts (GOP, 2014-15; PSMA annual report, 2014-15)

Based on area under sugarcane crop, production and yield per hectare, Pakistan occupy 4th, 5th and 60th position in world. During the year 2010 national average sugarcane yield per hectare (50 tonnes) was noted low compare to China (77.14), India (70.62), Philippine (92.62), Thailand (92.64), Australia (75.51) and Egypt (105.21) respectively (Azam and Mukarram, 2010). Average per hectare yield from 1998-99 to 2013-14 was highest in Sindh (55) followed by Punjab (49) and Khyber Pakhtunkhwa (45) (PSMA, 2014-15).

Per capita sugar consumption in Pakistan has increased from 22.71 kg in 2001-02 to 24.00 in 2014-15 which is largest in South Asia, where it is 14 kg in India, 10 kg in Bangladesh and 11 kg in China (Azam and Mukarram, 2010; PSMA, 2014-15).

Khyber Pakhtunkhwa is the third largest provincial economy of the country, it share respectively 9.5 and 9.7 % area and production of sugarcane crop at national level (Khan et al., 2012). Sugarcane yield level in Khyber Pakhtunkhwa is (45 tonnes/hectare) below the national average and other provinces of Pakistan (Tahir et al., 2014).

Because of passing-on from generation to generation sugarcane production is prominent in farming community, however its production in not mechanized and still labour intensive. Growers follows traditional practices and have low knowledge about pre-harvest practices such as proper use of FYM, chemical fertilizer, pesticides, inter-culturing, and timely irrigation. Also growers face post-harvest losses due to improper handling and harvesting (Nazir et al., 2013).

Yield gap in production between actual and potential was the main motivation for this study. This study contributes both to the analysis of technical efficiency and factors responsible for inefficiency in sugarcane production of study area. The study could guide resource utilization that can therefore lead to considerable resource saving.

Efficiency and productivity analysis has important implication for both policy formulation and farm management (Bravo and Riegler, 1991). Investigating low yield for brining efficiency in agriculture sector can improve overall living standard of farming community (Ali et al., 2013).

After introduction and objectives in section first rest of the paper is divided into four sections. Conceptual framework has been described in section two. Section third illustrates data and methodology. Results and discussions are given in section four. In section five conclusion and policy implications from the results are drawn.

The conceptual model

Technical efficiency represents the ability of a firm/farm to employ best practices and operate on the production frontier (Effiong and Onyenweaku, 2006; Greene, 2008). To build on this definition, this study is underpinned by Farrell (1957) model that explains measurement of technical efficiency in simplicity. According to Farrell (1957) a given firm is technical efficient if it correctly specify inputs set for its outputs. His basic idea regarding efficiency measurement is illustrated in Figure 1 that represents the case of multi-input and single-output constant returns-to-scale. Two inputs X1 and X2 are represented on horizontal and vertical axes respectively. The iso-quant SS/ represent different inputs combinations for a given amount of output Y. Producer on isoquant SS/ is considered technically efficient in his production process. Suppose a firm at point “P” produces the same amount of output “Y” as on isoquant SS/. For efficiency analysis of observed firm, a line from origin to the point P is drawn that intersect the isoquant at point “Q”. It can be seen that it produces same output using more inputs OP than desired level OQ. An efficient firm produce the same output (Y) at point Q/. The ratio TE = OQ/OP (ratio of distance from origin to point Q over point P) is used to defined technical efficiency of the observed firm at pint P.

Following Farrell (1957) model allocative efficiency can be measured from same diagram. Optimal pint is obtained where the isoquant curve is tangent to the budget line that is represented by point Q/ where the cost of production would be minimum.

Materials and Method

A formal survey was conducted in three districts (Mardan, Charsadda, and D.I.Khan) of Khyber Pakhtunkhwa. These districts are agrarian in nature and famous for the production of sugarcane crop. These districts share respectively 77.53 % area and 73.79 % sugarcane production at overall provincial level during the year 2014-15 (Govt. KPK, 2015). Geographical location of these districts gives fair representation to each zone of the province.

Source: Farrell, 1957

Respondents were selected through multi stage sampling technique. After purposive selection of above mentioned districts three tehsils (Takhbhia, proper Charsadda and Paharpur) were randomly selected each from one district respectively at stage-II. At stage-III respectively one union council (Shergarh, Muhammad Nahri and Kirrikhasor) was selected from aforementioned tehsils. Two villages given in Table 1 from each union council were randomly selected in stage –IV. At stage-V a sample size of 303 respondents was arrived by using the formula provided by Yamane (1967) given in equation 1.

 

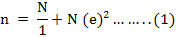
Where:

N: sample size ; N: population size: 1260; E: level of precision: 0.05.

Putting the values of “N and e” in equation 1 to sample size

n=1260/1+1260(0.05)2=303

Out of 303 sample size respondents from each districts were selected through proportional sampling allocation technique developed by Cochran, 1977 given in equation 2. This approach has also been applied by Oyethrough wo (2011) and Latt et al. (2011) in their studies.

 

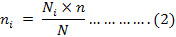
where:

ni: Number of sugarcane growers randomly interviewed in selected villages; Ni: Number of total sugarcane growers; n: Sample size for the study, N: Total number of sugarcane growers in the study area.

Table 1 presents numbers of respondents selected from each village through formula given in equation 2. List of total sugarcane growers in selected villages was obtained from Directorate of Agricultural Extension.

Analytical frame work

Efficiency measurement techniques can be broadly divided into parametric and non-parametric approaches. Parametric approach is based on econometric estimation of a production frontier whose functional form is specified in advance. It takes into account the random effect and inefficiency component. While in non-parametric techniques no functional form is imposed and it work under the assumption of no random shocks in data set (Vasilis, 2002).

Literature reveals that econometric method has been widely used to estimate technical efficiency in agriculture. Aigner et al. (1977) applied the stochastic frontier production function in the analysis of the U.S agricultural data. Battese and Corra (1977) applied the technique to the pastoral zone of eastern Australia. In Meeusen and Van (1977) application, the technique was applied to the analysis of ten French manufacturing industries. And more recently, empirical analyses have been reported by Battese et al. (1993), Ajibefun and Abudulkadri (1999) and Ojo (2004).

The stochastic frontier production approach

Almost for the first time Farrell (1957) introduced methodology to measure technical efficiency. Following Farrell pioneer work various improvement and modification have been made. Aigner et al. (1977), Meeusen and van (1977) and Battese and Corra (1977) are considered pioneers for stochastic frontier

Table 1: Distribution of sample sugarcane grower in study area

District	Union Council	Villages	Total growers	Sample size in each village	Sample size in each district
Mardan	Shergarh	Qasim khan Bandha	254	61	109
		Shaikhan kali	198	48
Charsadda	Muhammad Nahri	Sirdehri	269	64	118
		Sheikhabad	223	54
DIKhan	Kirrikashor	Umerkhela	205	49	76
		Shanki	111	27
Total			1260	303	303

Source: Directorate of agricultural extension, Government of Khyber Pakhtunkhwa, 2015

analysis approach. They independently proposed the general stochastic frontier production function given in equation 3 that account both the random error and inefficiency component specific to every producers.

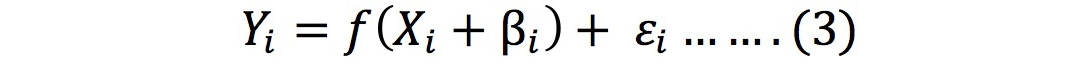
(i = 1, 2, 3…………..n)

Where:

Yi: ith farmer yield, Xi: represents inputs applied by ith farmer, β: Vector of unknown parameters in the model to be calculated, εi: ˅i - µi (error associated with ith farmer). ˅i ranges from - ∞ to ∞ that represents component of symmetric error. It accounts for weather, natural disasters, omitted variables, luck, exogenous shocks, measurements error and other statistical noise. It is assumed to be identically, independently and normally distributed as N(0,σ2 ˅ ). The term µi represents technical inefficiency of the ith farm that carries only positive values (Neff et al., 1993). It assumes half normal, exponential, truncated normal or gamma distribution (Stevenson, 1980; Aigner et al., 1977; Meeusen and Broeck, 1977). The term ˅i and µi are assumed to be independent of inputs used.

In this study stochastic frontier approach was employed, the choice was on the basis of variability in agricultural production because of climatic factors and non-availability of accurate farm data. SFA simultaneously take into account the random error and the inefficiency component specific to every grower (Ali et al., 2013). Several researchers such as Shamsudeen et al. (2011), Seidu (2012) and Donkoh et al. (2013) has also applied this approach for various crops in agriculture sector.

Model specification

In the present study proposed model for technical efficiency was put forward within the framework of Cobb Douglas production function. Following Battese and Coelli (1995), model given in equation 4 was estimated using maximum likelihood estimate (MLE) procedure. Following their specification a Cobb-Douglas type stochastic production frontier model is fitted to data as under,

 

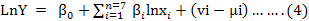
Where:

Yi: Yield of sugarcane in kg per acre, X1: Total area planted with sugarcane (in acres), X2: Sugarcane used for seed purpose in kg per acre, X3 : Chemical fertilizer (urea) applied in kgs per acre, X4: Chemical fertilizer (DAP + Potash) applied in kgs per acre, X5: Farm yard manure applied in Kgs per acre, X6: Tractor hours per acre, X7: Numbers of irrigation applied during entire season, X8: Pesticides/weedicides applied in milliliter per acre; X9: Labor man days per acre; X10: Dummy variable D1= 1 if farmer belongs to district Mardan otherwise 0; X11: Dummy variable D2 = 1 if farmer belongs to district Charsadda other wise 0; vi - µi: Represent composite error term.

The terms, n, β 0 and βi represents natural log, intercept and Parameters to be estimated.

The Maximum Likelihood Estimates (MLEs) of equation 4 provides rational estimates for β, γ and σ2 parameters, where σ2 describes the variation in the dependent variables due to random shocks (σ2 V) and grower inefficiency (σ2 u) together (Abdullah et al., 2006). Gamma (γ) interpret inefficiency in the overall variance with range between 0 and 1 (Coelli et al., 2005; Idiong, 2007; Abedullah et al., 2006). If γ is equal to zero, all deviation from the frontier is due to noise, while when γ is equal to 1 means all deviation is due to technical inefficiency (Coelli et al., 2005).

Model for estimation of technical inefficiency

(T. inefficiency)

Technical inefficiency model assumed normal distribution of vi i.e. N (0, σ2v) and half normal that of µi as N(0, σ2u ).Technical inefficiency of sugarcane grower was estimated by using the equation 5 given below:

 

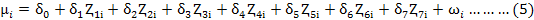
µi: Technical inefficiency associated with each farm/grower; Ⱬ1i: Age of sugarcane grower (years); Ⱬ2i: Experience (years); Ⱬ3i: Education (years); Ⱬ4i: Farmer family size; Ⱬ5i: Farmer contact with extension workers; Ⱬ6i: Distance between farm and house; Ⱬ7i: Dummy for off-farm income, D = 1 if farmer have off-farm income, otherwise 0; ωi: Error term assumed to be normally distributed i.e. N (0, σ2); δ0 and δi: represents parameters to be estimated.

Technical efficiency scores for ith farm

Stochastic frontier production function model has the advantage that along with determinants it allows for simultaneous estimation of individual respondent technical efficiency (Battese and Coelli, 1995). Technical efficiency of ith sugarcane farm was estimated by equation 6 given below. Ali and khan (2014) has also tried this in their research study.

 

 

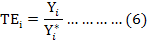
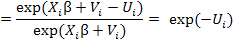
Where:

Yi: Observed yield of ith farmer; Y*i: Frontier yield ith farmer; TEi: Technical efficiency having ranges between 0 to 1.

Technical inefficiency of respective individual sugarcane grower was calculated by following formula:

T. inefficiency: 1-Technical.efficiency; T. inefficiency: 1- (Observed output / Frontier output), Technical inefficiency ranges between 0 and 1.

Validity of model assumptions

For validity of model assumptions it is of interest to test the hypothesis of normality, homoscedasticty and no multicollinarity in data set. Jarque-Bera , Brush-Pagan and Variance inflation factors (VIF) tests were tried respectively for normality, hetroscedasticity and multicollinearity in the data set. These tests are described below.

Normality test

The Jarque- Bera that is large sample test with two degree of freedom and follow chi-square distribution was apply to test normality of data. Null hypothesis specifies normal distribution of error term. Jarque-Bera test formula JB = n[{Sk2/6} + {Kr-3}2 /24}] was applied for normality. Symbols n, S and K represents sample size, skewness and kurtosis coefficient respectively (Gujarati and Porter, 2009). The estimated chi (2) = 0.087 is high than normal value of α = 0.05 which suggest that we cannot reject the null hypothesis that data is normally distributed.

Heteroscedasticity tests

The heteroscedastcity is a phenomenon where the stochastic random disturbance exhibit a non-constant conditional variance. Mostly cross sectional data has problem of heterogeneity compared to time series (Gujarati, 1985). Breusch-Pagan test with null hypothesis of constant variance was applied for heteroscedasticity. Calculated chi square value 2.83, with P value of 0.182 which is greater than 0.05 hence data has no heterogeneity problem.

Multicollinearity

If refers to the existence of linear relationship among some or all explanatory variables included in the model. It increase estimator variance, enlarge confidence interval, give high value of R2 with insignificant t-ratios (Gujarati, 1985). Variance inflation factors (VIF) was used that measure how much the variance of the estimated regression coefficients are inflated as compared to when the explanatory variables are not linearly related. VIF value of 3.52 illustrate that there is no problem of multicollinearity in the data set.

Results and Discussion

Table 2 describes data on output and input variables of 303 sugarcane growers that was analyzed by stochastic frontier production function approach.

The average sugarcane yield in study area was 23095.48 kg with standard deviation of 2117.45, which show large variability of yield among sugarcane growers. Average quantity of seed, urea, DAP and farmyard manure were estimated at 2821.37, 109.04, 81.94 and 1568.92 kg respectively. Mean farm size was 3.32 acres having standard deviation of 2.36. On average tractor hours applied were 22.66 with standard deviation of 6.24 up to maximum 43.70 hours per acre. During entire season maximum numbers of irrigation applied were 27. Average human labour (both family and hired) was 49 man days, with minimum and maximum rate of 36 and 68 man days respectively. It indicates that sugarcane production is water as well as labor intensive crop. Average pesticides application per acre in study area was 3627.06 milliliter up to maximum 7266.67 milliliter. Variability by standard deviation implies that growers operated at different level of inputs which affect their yield level.

Table 2: Description of variables considered for technical efficiency analysis

Variables	Unit	Mean	Std. Deviation	Range
				Minimum	Maximum
Yield	Kg	23095.48	2117.45	18746.67	27213.33
Seed	Kg	2821.37	379.87	1880.00	3360.00
Land USC	Acre	3.32	2.36	0.73	9.4
Urea	Kg	109.04	26.01	64.67	174.00
DAP	Kg	81.94	13.49	55.33	127.67
FYM	Kg	1568.92	300.82	1040.00	2192.33
Tractor hrs	Hrs	22.66	6.24	15.63	43.70
Irrigation	No	16.35	2.99	9.33	26.67
Pesticides	Ml	3627.06	1155.77	1966.67	7266.67
Labor days	MD	48.82	6.05	35.67	67.67

Kg: Kilogram; USC: Under sugarcane crop; Hrs: Hours; No: Number; Ml: Milliliter; MD: Man Days

Source: Author own survey, 2014-15

In study area grower’s average age was 39 years with wide variation, ranging from 18 to 67 years. Average formal education was 5.2 years with standard deviation of 3.49 years, which shows that growers were educated at primary level. Average farming experience was 12 years with significant variation from 2 to 30 years. Average household size is 10.267 members with standard deviation of 3.189. Mean value for contacts with extension workers and distance between farm and home was 7.142 numbers and 623.150 meters. Mean value for off-farm income was 0.51, which show that almost 51% growers has off farm activities.

Log likelihood ratio test for selection of functional form

The general Likelihood Ratio (LR) test was apply to test the presence of technical inefficiency effects. Null hypothesis or restricted model assumes no variation in output due to technical inefficiency that is ϒ = 0, while the alternative hypothesis was general stochastic frontier model assume ϒ is not equal to zero. LR test formula used was:

LR = - (log likelihood H0 - log likelihood H1)

This likelihood ratio test follow mixed Chi-square (χ2R) distribution, R represents numbers of parameters that are assumed zero in the null hypothesis or the number of parameters included in the unrestricted model (Rahman, 2003; Kolawole, 2006). Null hypothesis (H0) is to be rejected if LR test is greater than the critical Chi-square Table 3 value (LR > χ2R). In present study null hypothesis regarding no technical inefficiency effects is described below:

H0 = ϒ = δ0 = Respondent age = Education = Experience = Family size = Contact with extension workers = Off-farm income = Distance between house and farm = 0.

Table 3: Descriptive statistics of variables considered for technical inefficiency model

Variable	Mean	Std. Deviation	Minimum	Maximum
Age	39.389	11.871	18.00	67.00
Education	5.211	3.490	1.00	14.00
Experience	12.782	7.021	2.00	30.00
Family Size	10.267	3.189	4.00	18.00
Contact with Extension workers	7.142	2.808	2.00	21.00
Distance between home and field	623.150	263.858	150.00	1890.00
Off-farm income	0.510	0.500	0.00	1.00

Source: Survey data, 2014-15

The value of log-likelihood function for stochastic frontier production function was 35.40 and the value of log-likelihood function for restricted or ordinary least square (OLS) model was 57.03. The calculated generalized likelihood ratio test would be LR = -2 (35.40-57.03) = 43.26. Corresponding tabulated value is 14.07 when R or number of parameters assumed to be zero is 07. The tabulated value is less than calculated value i.e. 43.26. Null hypothesis of no technical inefficiency effects among the sugarcane growers is rejected at the 5 % significance level in favor of the presence of technical inefficiency effects among the farmers. This implies that Cobb-Douglas stochastic frontier model was fitted and adequate for representation of data.

Table 4: MLE estimates of stochastic frontier production function (SFPF)

Variable	Unit		Parameters			Coefficient	Standard error	T-ratio
Constant			β0			3.749	.210	17.81
Ln land USC	Acre		β1			0.053	0.018	2.94
Ln Seed	Kg		β2			0.103	0.028	3.67
Ln Urea	Kg		β3			0.068	0.021	3.27
Ln DAP	Kg		β4			0.020	0.011	1.85
Ln FYM	Kg		β5			0.024	0.014	1.65
Ln Tractor	Hrs		β6			0.111	0.029	3.80
Ln Irrigation	No		β7			0.118	0.026	4.54
Ln Pesticides	ML		β8			0.005	0.004	1.15
Ln Labor	MD		β9			0.121	0.413	2.94
Dummy 01			β10			-0.017	0.0104	-1.65
Dummy 02			β11			-0.082	0.017	-4.60
Inefficiency model estimates
Intercepts					δ0	-3.983	0.875	-4.55
Grower’s age		Year			δ1	-0.230	0.056	-4.14
Experience		Year			δ2	-0.065	0.032	-2.03
Educational level		Year			δ3	0.871	0.237	3.67
Farmer’s Family size		No			δ4	-0.021	0.0639	-0.34
Extension contacts		No			δ5	-0.164	0.0788	-2.09
Farm to home distance		Meter			δ6	0.00018	0.00076	0.24
Off- farm income		Dummy			δ7	-0.068	0.365	-0.19
Sigma-U					σµ	0.033
Sigma-V					σv	0.042
Lambda –λ(σµ/σv)						0.78
Gamma(σ2µ/σ2µ + σ2v)					ϒ	0.43
Technical Efficiency (TE)
Mean				Xmean(TE)		0.84
Minimum				Xmin		0.47
Maximum				Xmax		0.98

Ln: natural log; Kg: Kilogram; No: numbers; MD: Man Days; Rs: Rupees

Source: Own estimates, Survey data 2014-15

Maximum likelihood estimates (mle) results of the sampled farmers

MLE estimates of the stochastic frontier production function were arrived by using the computer software (STATA). MLE of parameters of SFA model along with those of inefficiency model are presented in Table 4. Positive as well as significant coefficients of land, seed, urea, DAP, farmyard manure, tractor hours, irrigation, pesticides and labor implies that per unit increase in these explanatory variables may enhance per unit yield of sugarcane crop. Negative signs for Dummy 01 and Dummy 02(-1.65 and -4.60 respectively) implies low yield level of sugarcane in District Charsadda and D.I. Khan compare to District Mardan. Results further illustrates that yield difference is not significant between district Mardan and Charsadda while it is significantly low in district D.I. Khan compare to these two districts. SFA values for elasticities of explanatory variables shows that one percent enhancement in allocation of land under sugarcane, seed, urea, DAP, FYM, tractor hrs, irrigations, pesticides, labor would rise the sugarcane yield by 0.053, 0.103, 0.068, 0.019, 0.087, 0.111, 0.118, 0.021 and 0.121 percent respectively. The coefficient of DAP, FYM and pesticides were positive but not significant at 5% significance level.

The technical efficiency scores of sample farms presented in Table 4 shows variation from minimum 47% to maximum 98% with the mean efficiency level of 84%. The mean technical efficiency implies that the average farm produces 84% of the maximum attainable with given inputs levels. Instant study mean value of technical efficiency revealed that it is in line with the findings of Ali and Chaudhary (1990) 87%, Murthy et al. (2009) 89%, Javed et al. (2008) 83%, Rangalal et al. (2013) 79%, Philips et al. (2012) 86%, and Ali et al. (2013) 77%.

Sources of technical inefficiency

Estimates for inefficiency parameters are incorporated in Table 4. Negative sign of parameter means that the associated variable has direct relationship with efficiency. The results indicated that the coefficient of grower age carry negative sign and is significant at 5% level. Age of grower play important role in decision making and has contribution towards grower general learning and correct judgment. Results show that as age of grower increase inefficiency decline, this may be due to managerial skills acquired by the grower over time. Our result is in line with Beniam et al. (2004).

Another important variable in inefficiency model is the grower’s experience, which carry negative sign and is significant at 5% level. Results imply that increase in duration of farmer’s involvement in sugarcane production increase the productivity and efficiency. Result is in line with Padilla et al. (2001) and Abedullah et al. (2006).

The coefficient of education has positive and significant relation with technical inefficiency. This implies that increase in formal education would increase inefficiency or decrease the production efficiency. It may be that farmers are using traditional methods that require no formal education or people get educated finds off-farm income opportunities and give less attention to farming. The finding is in line with Musab and Bwacha (2010).

The Coefficient for household size is negative and non-significant. This implies that in study area family size do not contribute in enhancing technical efficiency. Coefficient of contact with extension worker is significant and negative, it implies that grower technical inefficiency decrease with increasing contacts with extension workers. The result is in line with Dawang (2006).

The coefficient of distance between farm and house is positive but non-significant. It implies that distance between farm and house has no effect on grower productivity. In addition the coefficient of farmer participation in off-farm employment is negative but not significant. In this connection literature offers mix results. Abdulai and Huffman (2000) were of the view that off-farm activities reduce farm labor availability that effect technical efficiency. On the other hand Pascaul (2005) and Tesfay et al. (2005) reported direct relationship between off-farm employment and technical efficiency.

Gamma (ϒ) value 0.43 suggests that 43 percent variation in sugarcane yield is due to the differences in technical efficiencies and existence of inefficiency in the sampled farmers. Lambda (λ) value of 0.78 describes that in total deviation 78% difference between observed and maximum frontier yield is due to inefficiency among the sample respondents.

Conclusions and Recommendations

According to the empirical study, measurement of technical efficiency has been one of the most important issue of sugarcane grower for efficient use of resources in production. This study predict the level of technical efficiency of sugarcane growers and also explain variation in technical efficiency among farmers due to various socio-economic characteristics. In the frontier production function, the estimated coefficients for land, seed, urea, tractor hours and labor were found positive and significant at 5% significance level. However, coefficient for DAP, farmyard manure and pesticides was positive but statistically non-significant. Findings of the study illustrate high responsiveness of sugarcane crop to labor followed by irrigation, tractor hours, seed quantity, farmyard manure, urea, land, pesticides and DAP fertilizer. It suggests that the contribution of labor with elasticity of 0.121 is dominant factor which confirms that sugarcane seems to be labor intensive crop. The results of mean technical efficiency (84%) illustrate that there is scope for farmers to increase sugarcane yield by improving their resource use efficiency with the current technology.

Given the empirical findings, the suggestions and recommendations were proposed as following: the balance use of seed, urea, tractor hours, labor and timely application of irrigation water would increase per acre sugarcane yield. In the short run proper extension services with equipped skills may assist farmers to be better decision makers of their farms that ultimately decrease the level of technical inefficiency. Many of the farmers achieving high and consistent yields and then obtaining high technical efficiencies can be used effectively to demonstrate the benefits of good farming practices for reduction of gap between the actual and potential yield. Farmer’s specific to crop training, timely availability of inputs at reasonable price and effectiveness of extension services for farming community will help to decrease the gap between actual and potential.

Author’s Contribution

Amjad Ali collected and anlysed data and wrote the manuscript. Dr. Abbasullah Jan prvided technical input and guidance at every step.

References

Abdulai, A. and W.E. Huffman. 2000. Structural adjustment and economic efficiency of rice farmers in Northern Ghana Economic Development and Cultural Change. 48(3): 503-520.

Abedullah, B.K. and B. Ahmad. 2006. Technical efficiency and its Determinants in Potato Production, Evidence from Punjab, Pakistan. Lahore J. Econom. 11(2):1-22.

Ahmad, R., M. Saleem and M. S. Nazir. 1991. Autumn rationing potential of five sugarcane varieties. Pakistan J. Agric. Res. 13:26-30.

Aigner, D.J., C.A.K. Lovell and P. Schmidt. 1977. Formulation and estimation of stochastic production function models. J. Econom. 6: 21-37. https://doi.org/10.1016/0304-4076(77)90052-5

Ajibefun, I.A. and A.O. Abudulkadri. (1999). A Meta-analysis of technical efficiency studies in Nigerian agriculture. Paper presented at the International Association of Agricultural Economists 2009 Conference, August, 16 – 22, Beijing, China.

Ali, G., S.M.A. Shah., D. Jan., M, Fayaz., I.Ullah and M.Z. Khan. 2013. Technical efficiency of sugarcane production in district Dera Ismail Khan. Sarhad J. Agric. 29(4): 585-590.

Ali, S. and M. Khan. 2014. Technical efficiency of wheat production in District Peshawar, Khyber Pakhtunkhwa, Pakistan. Sarhad J. Agric. 30(4): 433-441.

Ali, M. and M.A. Chaudry. 1990. Inter-Regional farm efficiency in Punjab, Pakistan: a frontier production function study. J. Agric. Econom. 41: 62-74. https://doi.org/10.1111/j.1477-9552.1990.tb00619.x

Azam, M. and M. Khan. 2010. Significance of the sugarcane crops with special reference to NWFP. Sarhad J. Agric. 26(2): 289-295.

Backman, S., K.M. Zahidul-Islam and J. Sumelius. 2011. Determinant of technical efficiency of rice farms in North-Central and North-western regions of Banglash. J. Develop. Areas. 45(1): 73-94.

Battese,G. E. and G.S. Corra. 1977. Estimation of a production frontier model: with application to the pastoral zone of Eastern Australia. Aust. j. Agric. Res. Econom. 21(3): 169-179. https://doi.org/10.1111/j.1467-8489.1977.tb00204.x

Battese, G.E., S.J. Malik and S. Broca. 1993. Production functions for wheat farmers in selected districts of Pakistan: An Application of a Stochastic Frontier Production Function with time–varying inefficiency effects. Pak. Develop.Rev. 32: 233–68.

Battese, G.E. and T.J. Coelli. 1995. A model for technical inefficiency effects in a stochastic frontier production function for panel data. Emp. Econ. 20: 325-32.

Beniam, N.J., J. Tonye., N. Wandji., G. Nyambi, and M. Akoa. 2004. Factors affecting the technical efficiency among smallholder farmers in the slash and burn agriculture zone of Cameroon.

Bravo-Ureta, B. and L. Rieger. 1991. Dairy farm efficiency measurement using Stochastic Frontiers and Neoclassical Duality. Am. J. Agric. Econom. 73: 421-428. https://doi.org/10.2307/1242726

Chakraborty, K., B. Biswas and W. C. Lewis. 2001. Measurement of Technical Efficiency in public education: A stochastoic and nonstochastic production function approach. South. Econom. J. 889-905.

Cochran, W.G. 1977. Sampling Techniques, 3rd Edition. John Wiley and Sons, New York. pp. 37-45.

Coelli T.J., D.S.P. Rao, J. O’Donell and G.E. Battese. 2005. An introduction to efficiency and productivity analysis. 2nd ed., Springer, USA.

Dawang, N.C. 2006. Efficiency analysis of local chicks multiplication and production system in Plateau State, Nigeria, M.SC. Thesis, Department of Agricultural Economics Ahmadu Bello University, Zaria, Nigeria.

Debertin, D.L. 2012. Agricultural Production Economics, 2nd Edition. Macmillian Publishing Company, New York.

Donkoh, S.A., S. Ayambila and A. Shamsudeen. 2013. Technical efficiency of rice production at the Tono irrigation scheme in northern Ghana. Am. J. Exp. Agric. 3(1): 25-42. https://doi.org/10.9734/AJEA/2013/1448

Effiong, E.O. and C.E. Onyenweaku. 2006. Profit efficiency in broiler production in Akwa Ibom state, Nigeria. Int. J. Agric. Rural Dev. 7(1): 72-79. https://doi.org/10.4314/ijard.v7i1.2621

Farrell, M.J. 1957. The measurement of productive efficiency. J. Roy. Stat. Soc. Ser. A. 120: 253-90. https://doi.org/10.2307/2343100

Food and Agricultural Organization (FAO). 2014. Year wise world Sugarcane Statistics, http://ww.faostat.fao.org

Government of Khyber Pakhtunkhwa. 2014-15. Crop Reporting Services. Agriculture Livestock and Cooperation Department.

Government of Pakistan .Pakistan Economic Survey 2014-15. Ministry of Finance, Economic Advisor’s wing, Islamabad Pakistan.

Greene, W.H. 2008. The Econometric Approach to Efficiency Analysis. The Measurement of productive efficiency and Productivity Change. 92-250.

Gujarati, D.N. 1995 Basic Econometrics, 3th Edition. Mc Graw Hill Inc., New York.

Gujarati, D.N. and D.C. Porter. 2009. Basic Econometrics, 4th Edition. Mc Graw Hill Inc., New York.

Idiong, I.C. 2007. Estimation of Farm Level Technical Efficiency in small-scale Swamp Rice Production in Cross River State of Nigeria: A Stochastic Frontier Approach. World J. Agric. Sci. 3(5): 653-658.

Javed, M.I., S.A. Adil., M.S. Javed and S. Hassan . 2008. Efficiency Analysis of Rice Wheat System in Punjab, Pakistan. Pak. J. Agric. Sci. vol. 45(3).

Khan, B.M., Rahid and Q. Abdual. 2012. Response of new sugarcane genotypes in Southern Region of Khyber Pakhtunkwa. Pak. Sugar J. April-June.

Kolawole, O. 2006. Determinants of Profit Efficiency among Small Scale Rice Farmers in Nigeria: A Profit Function Approach. Poster Paper Prepared for Presentation at the International Association of Agricultural Economists Conference Gold Coast, Australia.

Latt, K.A., K. Hotta and T. Nanseki. 2011. Analysis of technical efficiency of monsoon rain-fed sesame production in Myanmar: A Stochastic Frontier Approach. J. Fac. Agr. Kyusha Univ. 56(1): 177-184.

Mceusen, W. and J. van den Broeck. 1977. Efficiency estimation from Cobb-Douglas production function with composed error. Int. Econom. Rev. 18: 435-44. https://doi.org/10.2307/2525757

Murthy, D.S., M. Sudha., M.R. Hegde., V. Dakshinamoorthy. 2009. Technical efficiency and its determinants in tomato production in Kamataka, India: Data Envelopment Analysis (DEA) Approach. Agric. Econom. Res. Rev. 22: 215-224.

Musaba, E. and I. Bwacha. 2014. Technical Efficiency of small scale Maize production in Masaiti District, Zambia: A Stochastic Frontier Approach. J. Econom. Sustain. Dev. 5(4): 104-111.

Nazir, A.G., A. Jariko and M.A. Junejo. 2013. Factors affecting sugarcane production in Pakistan. Pak. J. Comm. Soc. Sci. 7(1): 128-140.

Neff, D., Garcia, P. and Nelson, C., 1993. Technical efficiency: a comparison of methods. J. Agric. Econ. 44, 479–489.

Ojo. S.O. 2004. Improving labour productivity and technical efficiency in food crop production: A panacea for poverty reduction in Nigeria. Food Agric. Environ. 2(2) :227-231.

Oyewo, I.O. 2011. Technical efficiency of maize production in Oya state, Nigeria. J. Econom. Int. finance.Vol.3 (4): 211-216.

Padilla, M.D. and P.L. Nuthall. 2012. Farm Size and its Effect on the Productive Efficiency of Sugarcane Farms in Central Negros area, Philippines: An application of Data Envelop Analysis. J. ISSAAS Vol. 18, No. 1:49-61 (2012).

Padilla-Fernandez, M.D. and P.L. Nuthall. 2009. Technical Efficiency in the Production of sugarcane in Central Negros area, Philippines: An application of Data Envelop Analysis. J. Int. Soc. Southeast Asian Agric. Sci. 15(1): 77-90.

Pakistan Sugar Mills Association, Annual Report 2014-15.

Pascual, U. 2005. Land use intensification potential in slash-and-burn farming through improvements in technical efficiency. Ecol. Econom. 52: 497–511. https://doi.org/10.1016/j.ecolecon.2004.09.012

Padilla-Fernandez, M.D. and P. Nuthall. 2001.Farmers’ goals and efficiency in the production of sugar cane: The Philippine case, Farm and Horticultural Management Group Lincoln University, ISSN 1174-8796, Research Report 07/2001.

Philips, N.O.O and J.A. Mbanasor. 2012. Analysis of the constraints and technical efficiency differentials among agribusiness firms in Nigeria. College of Agribusiness and Financial Management, Michael Okpara University of Agriculture, Umudike, Abia state Nigeria.

Rangalal, M. 2013. Farm level technical efficiency in paddy production: A translog frontier production function approach. Int. J. Adv. Res. 1(3):300-307.

Rehman, S., G.S. Khan and I. Khan, 1992. Coordinated uniform national varietal trial on sugarcane. Pak. J. Agric. Res. 13: 136-140.

Seidu, A. 2012. Technical efficiency in small paddy farms in Ghana: an analysis based on different farming systems and gender. J. Econom. Sustain. Dev. 3(5):91-107.

Shamsudeen, A., S.A. Donkoh and G. Sienso. 2011. Technical efficiency of groundnut production West Mamprusi district of Northern Ghana. J Agric. Biol. Sci. 2(4): 71-77.

Stevenson, R.F. 1980. Likelihood functions for generalized stochastic frontier estimation. J. Econ. 13:57-66.

Tahir, M., I.H. Khalil., P. McCord and B. Glaz. 2014. Character association and selection indices in Sugarcane. Am. J. Exp. Agric. 4(3): 336-348. https://doi.org/10.9734/AJEA/2014/6086

Tesfay G., R. Ruben., J. Pender and A. Kuyvenhoven. 2005. Resource use efficiency on own and Share cropped plots in Northern Ethiopia: determinants and implications for sustainability. Southeast Asian Agric. Sci. 15(1): 77-90.

Vasilis, S. 2002. An assessment of comparative efficiency measurement techniques. Occasional paper 2, European Economics London WC2 1QU.