Research Article

An Analysis of Energy Supply and Oil Price Shocks on Agricultural Productivity of Pakistan

Yasir Arafat1*, Syeda Nabahat2, Hafiz Ullah3, Afaq Ali Muluk4 and Azra5

1Department of Economics, University of Chitral, Khyber Pakhtunkhwa, Pakistan; 2College of Home Economics, University of Peshawar, Khyber Pakhtunkhwa, Pakistan; 3Department of Botany, University of Chitral, Khyber Pakhtunkhwa, Pakistan; 4Department of Economics, University of Chitral, Khyber Pakhtunkhwa, Pakistan; 5Department of Economics, Kohat University of Science and Technology, Kohat, Khyber Pakhtunkhwa, Pakistan.

Received | October 22, 2019; Accepted | October 03, 2020; Published | October 25, 2020

*Correspondence | Yasir Arafat, Department of Economics, University of Chitral, Khyber Pakhtunkhwa, Pakistan; Email: yasir.eco@uoch.edu.pk

Citation | Arafat, Y., S. Nabahat, H. Ullah, A.A. Muluk and Azra. 2020. An analysis of energy supply and oil price shocks on agricultural productivity of Pakistan. Sarhad Journal of Agriculture, 36(4): 1120-1126.

DOI | http://dx.doi.org/10.17582/journal.sja/2020/36.4.1120.1126

Keywords | Agriculture productivity, Energy supply, Oil price shocks, FDI, ARDL model

Introduction

Energy is one of the key factors in the development of agriculture and hence poverty alleviation in the country. Energy supply is a major problem of nearly all the developing countries of the world, which directly affects the economy in all dimensions (Ahuja and Tatsutani, 2009). The future growth of economy in any sector depends on the availability and provision of energy from accessible and environmentally friendly resources. Climate change, food security and public health are closely linked to energy supply (Owusu and Sarkodie, 2016). In almost all countries of the world it is considered an important factor not only to increase production per acre in agriculture but play a major role in enriching other sectors of the country as well. Thus, the life standard in a country can be directly related to the energy consumption per capita (Arto et al., 2016).

Almost 40 percent of the world’s population depends on agriculture as the chief source of income, many of which do not have an access to energy (UN, 2017). Crops management by farmers through conventional physical work is inconsistent and depends on weather conditions as compared to farmers with access to modern agricultural equipment. Improving agricultural productivity directly affects poverty reduction. According to an estimate 10 percent increase in agricultural productivity for small farmers in Pakistan leads to a 7 percent poverty reduction. It is also a key strategy to support countries most vulnerable to the effects of climate change (Ali et al., 2017).

Like other developing countries, Pakistan is also an agricultural country, where about 61 percent of work force is associated with this sector and it is considered as the life line for all economic activities (Lawal, 1997). Since its inception, Pakistan’s economy largely relies on this sector in order to earn sustainable inflow. The agricultural land in this region is highly fertile and best suited for cultivation for all varieties of crops. In most of the region traditional form of cultivation is still practiced which creates hurdles in per acre yield. According to agricultural experts, the unit area productivity is slightly decreasing in Pakistan owing to two reasons: the first being illiteracy and unawareness of farmers to use modern technology. The second reason according to them is the use of appropriate fertilizers and pesticides are very low in Pakistan due to income constraints face by the farmers (Ehimore, 2009). The agriculture sector all over the world has become highly mechanized but in Pakistan, the traditional tools and techniques are in use, which directly impair its productivity and cannot accomplish the demand of 210 million populations.

The history of agriculture in Pakistan shows that in the past, production increased mainly due to the expansion of the cultivated land by bringing barren land and deserts under cultivation. Studies on soil or cultivated crops have not been conducted in the past; a soil conservation strategy has not been adopted just because of low research and innovation in this field and lack of scientific experimentations. Pakistan has benefited significantly from suitable fertile soil for all types of crops that made the bulk of grain production. Although several studies on energy models have been conducted in Pakistan, projected to specific area and crop (Khan and Singh, 1996, 1997).

In recent years, increasingly concentrated settlement patterns and rising competition with other land uses have extensively reduced the area of agricultural land. As a result, the limited supply of fossil fuels is the most serious issue in Pakistan, despite its growing threat to the carbon greenhouse environment, global warming and energy crisis (Mohan, 2008).

Energy is generally considered as an important factor to accelerate economic activities which significantly influence high yield. High-quality energy resources can mediate technology, while less reputable sources can reduce the power of new technologies. Ojinnaka (1998) states that energy consumption is associated with an economic growth. According to him Per capita energy consumption is an important indicator of economic growth. Countries with higher energy consumption per capita are generally more developed as they can use it for more agriculture productivity than those with lower energy consumption per capita.

The cherished objective of this study is to examine the impact of supply of energy and oil prices on agriculture in Pakistan. Agriculture sector is considering the backbone of Pakistan economy but its share in total GDP is minimal as compare to other sector of the economy (Anwar et al., 2015). When structural changes occurred, the mechanization increased in agricultural sector. The energy input has increased in order to run agricultural machineries such as pipelines, tractors, and wake machines. Due to inadequate energy consumption per unit area, agricultural production has decreased (Kienzle et al., 2013).

Theoretical model

In growth theory, emphasis was made on two main inputs, namely labor and capital. The role of energy is considered insignificant and indirect in the process of production and growth. Oil, which are reserves, are considered the main sources of energy, but their role is not explicitly stated in the standard growth theory, which focuses only on capital and labor.

The mainstream neoclassical economist is convinced that the energy available at any time in the economy is endogenous, limited by various restrictions such as oil reserves, lack of established production, generation, refining and efficiency. All of these factors mitigate the effects of energy as a driver of economic growth and production.

The theoretical model for this study is based on endogenous growth model, presented by neoclassical economists. The function form of the model was presented by Ayres et al., 2009, given as under:

Y= f (A, K, L, μt) .… (1)

Where;

Y= Total Production; A= Total Factor Productivity; K= Capital; L = Labor; μt= Error term, that is normally distributed with mean zero (μ=0) and variance sigma square (σ2).

The above Equation 1 shows the production function. The difference between conventional production function and mainstream production function is that of “A”. In the above equation “A” is factor productivity, consists of tools and machinery but according to Neo-classical, mainstream Economist, it is the difference of Energy supply (Es) and energy demand (Ed), which they named as Energy balance (Eb= Es- Ed), according to them it can be used as proxy for “A”. So, the current study also taken energy supply, demand and energy balance as a function of “A”. Thus, Equation 1 can be written as:

Y= F (Ed, Es, Eb, K, L, μt) .… (2)

Where;

A= f (Ed, Es, Eb)

The above equation shows that when Energy supply (Es) and Energy demand (Ed) are equal, then the economy observes Energy balance (Eb) (Ayodele, 1998).

So, through the above model, the study has extracted the following information.

Y = f (Eb, K, L)

Thus, the model for this study is formulated on the basis of the above endogenous growth model presented by neoclassical Economists.

 

Material and Methods

In this study, time series data on agricultural productivity in Pakistan, energy supply, oil price shocks, and foreign direct investment between 1990 and 2017 is used. Using time series statistics helps us evaluate the effects of energy supply on cropped area and agricultural productivity over a specific period in order to increase yield per hectare. To this end, data from the Pakistan Bureau of Statistics, World Development Indicators and Pakistan Agricultural Statistics were collected over the same period. When analyzing time series data, problems of heteroscedasticity always exist (Frost, 2017). The study converted all the variables in to log form in order to avoid heteroscedasticity issue and then an econometric model is estimated.

Time series analysis uses a variety of methods to estimate data. All these methods are useful and should be followed accordingly; otherwise, the whole process will produce false results. Consequently, before estimating the data for integration, it is important to know the stability situation; Data should not have a problem of unit root. For this purpose, the present study uses Augmented Dickey Fuller (ADF) test in order to remove this problem from the data. It contains the following three models.

ΔA = β1 + ZAt-1 + α1 + µt ..…(3)

ΔA = β1 + β2 + ZAt-1 + α1 + µt ……(4)

ΔA = ZAt-1 + α1 + µt ..…(5)

In the above equations, there is only intercept in Equation 3. In Equation 4, both intercept and trend are included but both intercept and trend are missing in last equation i.e. Equation 5. These equations show the status of stationarity of variables. The aim of including these equations in the model is that if one of the above equation show non-stationarity of variable in any integration the variable is considered as non-stationary, so for stationarity all the above situation should be fulfilled otherwise the results will be ambiguous (Gujarati, 2014). In 1988, Peter C.B. Phillips and Pierre Perron presented their Phillips-Perron (PP) unit root test. Although the PP test is similar to the ADF test, both are used for unit root test. It was observed that the PP test ignore serial correlation, the ADF can use parametric auto-regression to target errors. Interestingly, both gave the same results, despite their differences.

The procedure of ADF is that one should check variables in level form, if the variable shows non-stationarity in the above three equations then we move to second step i.e. to check the variable in first difference in all three equations and will continue the process until we get stationarity of the variables in above three equations. If the variable is stationary at level, we call this integration of zero i.e. I (0), if it is stationary at first difference, then it is written as I (1). In case of second difference, we write it as I (2). While analysis time series, it is necessary to check stationarity of the data before estimation, the presence of unit root in the variable make the results spurious. To examine the issues related to the model, one should observe the value of Dickey Fuller (DF) test. The value must be negative in this case.

ARDL model

To reflect the impact of various long-term variables, co-integration criterion will be used. Granger (1988) use the method in order to know long-run association of variables. According to him co-integration among variables is only possible when they have long-run association otherwise not, this shows no association of variable, means they are totally different from one another (Dickey et al., 1979).

The present study is uses ARDL model suggested by Pesaran et al., 2001 in order to estimate the model with integration of 0 and 1. The unit root test shows that the variables in the model are integrated of 0 and 1, if no variable are stationary in level i.e. I (0), then we use VAR model, same is the case of VECM and other models. In this case this is best suited to know the relationship between agricultural productivity, energy supply, oil price shocks and FDI. Different methods and producers are being used by different researcher in the past to find integration among variable but this study use ARDL model because it is easy way to estimate single equation. The second reason is that it can estimate variables with different integrations as well. The model is also superior in the sense that it estimates small data-set and provide reliable outcomes (Pesaran et al., 2001).

Steps involve in ARDL model is given as under:

The first step involves to estimate the dynamics of short and long run parameters. Subsequently, through F-statistics, the long-run association among variables can be find out. For this purpose, test propose by Pesaran et al., 2001 i.e. Bound test can be used. If the model has a common integration between various variables, then we can convert the dependent variable as a long-term independent variable to find ECM (Error Correction Model). The equation of ARDL with the ECM of ARDL thus pass through heteroscedasticity, stability, normality, and correlation. tests to verify the correct functional form. The ARDL model is given as under:

Where;

Y is Agriculture productivity; αi, α0= Drift factor and white noise respectively; ES= Energy supply; FDI= Foreign direct investment; OP= Oil prices.

After all the processes are completed, we can use the F-based test to examine the long-term relationship between several variables (Pearson et al., 2001). The next step is to validate the notion that adopting a null hypothesis means that there is a cohesion hypothesis between the null hypothesis and that an alternative is accepted, which means that there is no integration. The null hypothesis H0.= α1.= α2.= α3. = 0. and the alternative hypothesis H1.: α1. ≠ α2. ≠ α3. ≠ 0. If the statistical value of F is greater than the critical value, at a critical point, we reject Ho and when the value is less then critical value, null hypothesis is accepted, which shows the presence of co-integration. Lastly, the error correlation method is written as:

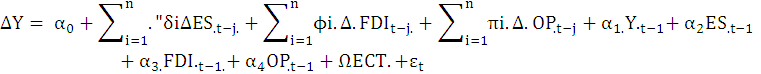
Ω in the above equation shows speed of adjustment and it value must be negative.

 

Results and Discussion

As discussed earlier, the important step dealing with time. series data is to know the stationarity of the variables. To know this, ADF model is use, which tell us wither there is a problem of unit root in the variables are not. The result of unit root test is presented in the Table 1. For studying trends in variables see Supplementary figures 1-4.

The results presented in the Table 1 show that two variables i.e. energy supply and oil prices are integrated at the level and agriculture productivity and FDI are integrated of 1. The Table 1 shows that variables are integrated at different integration, it means ARDL test is best option to analyze the data and to find-out possible association among them. The lag length is selected though AIC. The lag length for Y, ES, FDI and OP are 1, 0, 1.0 and 1 respectively.

Short-run and long-run estimation

After obtaining the integration order the second step is to know the existence of long-term and short-term relationships between different variables in the model. The study uses annual time series data for the time period 1990 to 2015, so, maximum of 2 Lag will be taken, this lag is typically small in order not to lose degree of freedom (Wooldridge, 2012). This evaluation method was proposed in 1999 by Pesaran and Shin and in 2004 by Nayaran. In addition, the study used the optimal number of lags to allow conditional error correction in the model, in order to ensure serial correlation problem in the model, proposed in 2001 by Pesaran, though Schwaez-Bayesian Information Criteria (SBC). The results are presented in the Table 2.

 

Table 1: Unit root test.

Variables	No of lags	Level form	First difference form	Order of integration
Agriculture productivity (Y)	2(AIC)	-2.245210	-4.656322**	I(1)
Energy supply (ES)	4 (AIC)	-3.338822		I (0)
FDI	6 (AIC)	-1.331184	-3.953766**	I (1)
Oil prices	2 (AIC)	-2.078340		I (0)

Source: Author’s calculations.

 

Table 2: Bound’s test for co-integration analysis.

Co-integrating Form
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(LY(-1.))	-0.251623	0.224125	-0.540887	0.5960
D(LY (-2.))	-0.538216	0.241351	-4.305236	0.0045
D(LES)	0.102435	0.014365	1.109868	0.2835
D(LFDI)	0.032435	0.015415	0.143168	0.0215
D(LOP)	0.016518	0.054162	2.702834	0.0157
Coint.Eq (-1)	-0.164327	0.042621	-3.344784	0.0041
Cointeq = LY - (0.5382*LES + 0.03243* FDI+ 0.3438*LOP + 0.032435)
Long Run Coefficients
Variable	Coefficient	Std. Error	t-Statistic	Prob
LES	0.536523	0.026376	7.153239	0.0000
LFDI	0.251321	0.161231	2.25236	0.0162
LOP	-0.456121	0.151601	2.35286	0.0173
C	3.991626	1.121087	3.560497	0.0026

 

Table 2 is estimated to know the existence of long and short run association between dependent and independent variables in the model. It depicts that when 1 percent increase in Energy supply in the long run, increases agriculture productivity by 0.54 percent likewise, FDI also effect Y positively, it shows that when FDI in agriculture sector increase by 1 percent, productivity will be going to increase by 0.52 percent. Oil price shocks effect productivity negatively. An increase in price by 1 percent. “decreases” productivity by 0.45 percent.

LM test for serial correlation

To know the existence of serial correlation in the model, the Table 3 is estimated through LM test:

 

Table 3: Serial correlation, LM test.

F-statistic	1.236125	Prob. F (2,18)		0.3052
Obs.*R-squared”	3.253712	Prob. Chi-Square (2)		0.1174
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LES(-1)	(-0).104721	0).263412	-0).647289	0.5947
LFDI	0).023416	0).134612	-0).229062	0.0237
LOP	-0).046275	0).158706	-0.524525	0.6071
C	-0).068053	.3.314470	-0.023405	0.9229
RESID(-1)	0).254266	0).305420	-0.834289	0.4184
RESID (-2)	0).352373	0).256374	-1.224139	0.2268

Source: Researcher’s calculations.

 

This Table 3 is intended find out Serial correlation in the model. The Table 3 depict that the model does not have serial correlation problem. The results of F-state and Prob Chi-Square are insignificant. The theory tells us that the null hypothesis shows serial correlation in the model and alternative hypothesis shows its existence. It shows that the model has no serial correction problem and the null hypothesis is rejected and Alternative is accepted.

Test for stability

To check the stability of variables in the model, CUSUM test and CUSUM of Square test is use. This indicates the instability and incorrect specifications of variables in the model. Looking at the Figures 1 and 2, in Figure 2, the line touches the lower bound but doesn’t crosses it means in the long run the variables remain stable. It becomes clear that the model has no stability problems and incorrect variable specifications. Both the figures show stability of the model.

Bound’s test for co-integration analysis

The results of co-integration analysis are presented in the Table 5 co-integration analysis tells us wither there is any long run association between variables or not. According to null hypothesis, there is no long run relationship. By looking the table below the value of F-statistic is 1.49 and value of lower bound and upper bound is 2.62 and 3.79 respectively at 5 Percent confident Interval because of lower F- value as compare to lower and upper bound statistic, we accept our null. hypothesis of not existence of co-integration among variables in the long-run.

 

 

 

Table 5: Co-integration analysis.

Test Statistic	Value	K
F-statistic.	1.49253	5
Critical value bounds
Significance	Lower bound	Upper bound
10 %	2.26	3.35
5 %	2.62	3.79
2.5 %	2.96	4.18
1 %	3.41	4.68

Source: Author’s estimates.

 

Conclusions and Recommendations

Our research work has revealed. the impact of energy supply and oil price hike on Pakistan’s agricultural productivity using data spread from 1990-2017. The data were collected from Pakistan Statistics Bureau, WDI and Pakistan Agricultural Statistics. Energy supply, foreign direct investment and oil prices are considered independent variables and are determinants of agricultural productivity in Pakistan. The ARDL was applied know the relationship between dependent and independent variables. It was established that energy supply and foreign direct investment influence agricultural productivity positively and significantly while oil prices negatively shape agriculture productivity in Pakistan. It was also observed that in Pakistan the use of modern agricultural tools and techniques is insufficient to boost up per acre yield. It is thus recommended that government and agriculture experts should focus on modern technology and provide farmers with high quality seeds. According to the result energy supply and FDI affect productivity positively, 1 percent increase in energy supply and FDI increases agriculture productivity by 0.52 and 0.54 percent respectively, indicating a higher energy input. Most of the farmers use oil-fueled generators to run their tube wells, which is not cost effective. An increase in oil price by 1 percent decreases productivity by 0.45, representing the need of cheaper sources of energy affordable to farmers.

 

Novelty Statement

The study has developed a new linkage between energy supply and agricultural productivity, imperative research to make crucial decisions in future.

 

Author’s Contribution

Yasir Arafat: Write up and analysis of the data.

Syeda Nabahat: Summary of literature review and conclusion.

Afaq Ali Muluk: Collected data related to supply of energy.

Hafiz Ullah: Collected data related to agriculture productivity.

Azra: Helped in overall format and improvement.

 

Supplementary Material

There is supplementary material associated with this article. Access the material online at: http://dx.doi.org/10.17582/journal.sja/2020/36.4.1120.1126

Conflict of interest

The authors have declared no conflict of interest.

 

References

Ahuja, D. and M. Tatstani. 2009. Sustainable energy for developing countries. Surv. Perspect. Integ. Environ. Soc., 2: 1.

Ali, S., Y. Liu, M. Ishaq, T. Shah, Abdullah and I.U. Din. 2017. Climate change and its impact on the yield of major food crops: Evidence from Pakistan. Food, 27 March, 2017. https://doi.org/10.3390/foods6060039

Anwar, M.M. and S. Farooqi. 2015. Agriculture sector performance: An analysis through the role of agriculture sector in GDP. J. Agric. Econ. Ext. Rural Dev., 3(3): 270-275.

Arto, I., I.C. Perez, G. Bueno and R. Bermejo. 2016. The energy requirements of a developed world. Energy Sustainable Dev., 33: 1-13. https://doi.org/10.1016/j.esd.2016.04.001

Ayres, R.U. and B. Warr. 2009. The economic growth engine: How useful work creates material prosperity. https://doi.org/10.4337/9781848445956

Ayodele, A.S., 1998. Energy crisis in Nigeria: The case of electric energy market: Bullion Publication of CBN, Vol.22 No. 4.

Dickey, D.A., and W.A. Fuller. 1979. Distribution of the estimators for autoregressive time series with a unit root. J. Am. Stat. Assoc., 74: 427–431. https://doi.org/10.1080/01621459.1979.10482531

Ehimore, O.M., 2009. Pre-Colonial nigerian economy: Dynamic or stagnant. http://www.articlesbase.com/authors/o.mehinmore/161024.htm

Frost, J., 2017. Introduction to statistics. An intuitive guide for analyzing data and unlocking discoveries.

Granger, C.W.J., 1988. Some recent development in a concept of causality. J. Econ. 39(1-2):199-211. https://doi.org/10.1016/0304-4076(88)90045-0

Gujarati, D., 2014. Econometrics by example. 2nd Edition. https://doi.org/10.1007/978-1-137-37502-5_1

Khan, M.A. and G. Singh. 1996. Energy inputs and crop production in Western Pakistan. Energy, 21(1): 45-53. https://doi.org/10.1016/0360-5442(95)00077-1

Khan, M.A. and G. Singh. 1997. Energy inputs and potential for agricultural production in western Pakistan. Agric. Syst., 54(3): 341-356. https://doi.org/10.1016/S0308-521X(96)00067-4

Kienzle, J., J.E. Ashburner and B.G. Sims. 2013. Mechanization for rural development. integrated crop management mechanization for rural development: A review of patterns and progress from around the world. Vol. 20–2013.

Lawal, A.A., 1997. The economy and the state from the pre-colonial times to the present in osuntokun, A. and Olukoju, A. (eds.) Nigerian peoples and cultures. Ibadan: Davidson.

Mohan, 2008. Anti-fertility activity of whole plant extracts of Polygala rosmarinifolia Wight and Arn against male albino rats VL- 3. J. Adv. Pharm. Sci.,

Ojinnaka, I.P., 1998. Energy crisis in Nigeria: The role of natural gas. CBN Bull., 22(4): 8–12.

Owusu, P.A. and S.A. Sarkodie. 2016. A review of renewable energy sources, sustainability issues and climate change mitigation. J. Cogent Eng., 3(1). https://doi.org/10.1080/23311916.2016.1167990

Pesaran, M.H., Y. Shin and R.J. Smith. 2001. Bounds testing approaches to the analysis of level relationships. J. Appl. Econ., 16(3): 289-326. https://doi.org/10.1002/jae.616

Pesaran, M.H. and R.P. Smith. 1998. Structural analysis of co-integrating VARs. J. Econ. Surv., 12: 471-506. https://doi.org/10.1111/1467-6419.00065

UN Report, 2017. The future of food and agriculture Trends and challenges. Food Agriculture Organization of the United Nation.

Wooldridge, J.M., 2012. Introductory econometrics: A modern Approach.