Predicting Honey Production using Data Mining and Artificial Neural Network Algorithms in Apiculture

Hide Journal Menu

<< Previous Article

Current Issue

Next Article >>

PJZ_49_5_1611-1619

Predicting Honey Production using Data Mining and Artificial Neural Network Algorithms in Apiculture

Koksal Karadas1* and Ibrahim Hakki Kadırhanogullari2

1Agricultural Faculty, Igdir University, Igdir 76000, Turkey

2Independent Researcher, Turkey

ABSTRACT

This survey was conducted on all the 85 beekeeping farms collected with census study method in Igdir province of Turkey with the purpose of determining some factors influencing average honey yield (AHY) per beehive in the year 2014. For this purpose, predictive performances of several data mining algorithms (CART, CHAID, Exhaustive CHAID and MARS) and artificial neural network algorithm (Multilayer Perceptron, MLP) were evaluated comparatively. Several factors thought as independent variables in the survey were age of beekeeper (AB), education level (EL), number of full beehives (NFB), bee race (BR), the time spent in plateau (TSP), feed of autumn and spring (FAS), working period in apiculture during year (WPA), frequency of changing queen (FCQ), and controlling beehives in summer (CFB), respectively. Minimum beekeeping farm numbers for parent and child nodes were arranged as 8:4 in CART, CHAID and Exhaustive CHAID for attaining the best predictive performance in AHY. In the Exhaustive CHAID, only 3 independent variables, NFB, WPA and CFB were found statistically. In the CART algorithm, only NFB, WPA and AB independent variables were found significantly. In the MARS algorithm, significant independent variables were determined to be some main and interaction effects of NFB, FAS, WPA, EL, AB, FCQ and TSP. The significant order of the Pearson coefficients between actual and fitted values in AHY was MARS (0.913a) > ANN (0.885ab) > Exhaustive CHAID (0.786b) > CHAID (0.769b) > CART (0.744). It was concluded that the MARS algorithm having the best predictive accuracy among all the algorithms might offer a good solution to beekeepers in describing interactions of significant independent variables.

Article Information

Received 01 February 2017

Revised 30 March 2017

Accepted 12 May 2017

Available online 11 August 2017

Authors’ Contribution

KK designed the experiment, acquired and analyzed the data and drafted the manuscript. IHK interpreted the data and helped in preparation of manuscript.

Key words

Beekeeping, Honey yield, Regression tree analysis, Data mining, Production economics.

DOI: http://dx.doi.org/10.17582/journal.pjz/2017.49.5.1611.1619

* Corresponding author: [email protected]

0030-9923/2017/0005-1611 $ 9.00/0

Introduction

Honeybees in apiculture are known as significant pollinators of crops and wild plants growing in nature and responsible for one third of plant related food production by means of the pollination (Klein et al., 2007; Pohorecka et al., 2014). Apiculture is one of the animal activity branches that have several advantages like gaining extra income source, being independent from soil, requiring less labor, generating income in a short time, and having lower investment costs. In apiculture, honey, pollen, royal jelly, bee venom and beeswax used for human nourishment, health and economic sectors are produced in the world. According to FAO (2013) records, number of beehives, total honey production, and honey yield per hive are 80 910 086, 1 663 798 tons, and 20.56 kg in the word, and corresponding values in Turkey are 6 641 348, 94 694 tons and 14.26 kg. Because of the fact that the lower honey yield amount per hive was produced in Turkey, further surveys on increasing the yield and detecting several decisive factors affecting the yield are still required.

Qaiser et al. (2013) highlighted the great importance of beekeeping due to economic benefits of those living in sustainable rural regions. In literature, several surveys on economic analysis of the beekeeping farms at various countries of the world have been conducted in order to reveal effectual factors affecting honey and other bee-products in recent years. Among the earlier surveys, Makri et al. (2015) economically analyzed efficiency of Greek beekeeping farms via data envelopment analysis. Poornima (2014) evaluated socio-economic factors of beekeeping in Uttara, Kannada, India and reported that it was a good family business on small and large scales with the aid of enhancing subsidy and loan. Cejvanovic et al. (2011) economically modeled sustainable beekeeping productions in Bosna and Hercegovina of the Balkan Peninsula. Kezic et al. (2008) economically assessed beekeeping in Croatia on the basis of number of bee hives, number of beekeepers, average number of bee hives, average yield of honey per hive, income from honey, basic price, selling price, productivity, and economic efficiency etc. Castellenos-Potenciano et al. (2015) made socio-economic characterization of beekeepers by means of principal component analysis and reported the data on characteristics of beekeeping production technology like total number of hive, total honey production, and total days working in apiculture, and total number of apiaries, etc. across the Gulf of Mexico. In Swaziland, Masuku (2013) defined socioeconomic characteristics of beekeeping in order to reveal the relationship between honey production and socioeconomic characteristics of the beekeepers via multiple regression analysis in the Manzini Region. Economically analyzing small beekeeping farms in five districts of Serbia, Marinkovic and Nedic (2010) addressed the data on number of beehives, type of product, and volume of production per hive etc. Vural and Karaman (2010) investigated socio-economic analysis of beekeeping as well as the influence of beehive types on honey production in Bursa province of Turkey.

Some authors addressed in apiculture literature in Turkey that there was lack of technical information in Hatay province (Sahinler and Sahinler, 1996) and Van province (Erkan and Askin, 2001) of Turkey, whereas the production and marketing problems were reported by Parlakay (2004) for Tokat province and Kekecoglu and Goc Rasgele (2012) for Duzce province of Turkey. Additionally, Uzundumlu et al. (2001) mentioned that climate condition adversely affected apiculture in Bingol province. In a survey conducted in Kirsehir province of Turkey, Tunca and Cimrin (2012) informed to be the adverse effects of bee diseases on honey yield. However, no survey was found on factors affecting the honey yield in beekeeping farms of Igdir province, which has a rich flora for beekeeping of the Eastern Anatolia of Turkey-neighbors with Armenia, Azerbaijan (Nakhchivan Autonomous Republic), and Iran-includes the Ararat Mountain (Eyduran et al., 2015a). Therefore, the present survey was conducted on all the beekeeping farms registered to Apiculture Association in Igdir province of Turkey in order to determine some factors influencing average honey yield per beehive (AHY). The second aim of the survey was to determine the best accuracy one among some data mining algorithms (CART, CHAID, Exhaustive CHAID and MARS) and artificial neural network algorithm (MLP) in predictive ability. We aimed to develop a useful model by means of the examined algorithms and, especially MARS algorithm.

Materials and Methods

A survey on all the 85 beekeeping farms registered to Igdir Beekeepers Association in Turkey was carried out to define significant factors influencing average honey yield per beehive (AHY, kg/hive) in the year 2014. The survey data were gathered with census study method from Igdir province.

Several potential factors thought as independent variables in the survey were age of beekeeper (AB; mean: 52, 25 to 80 age), education level (EL; illiterate(EL_1), literate (EL_2), primary school (EL_3), secondary school (EL_4), high school (EL_5), two-year degree (EL_6) and bachelor’s degree (EL_7)), number of full beehives (NFB; mean: 66, 20 to 260), bee race (BR, Caucasian (BR_1), Caucasian crossbreed (BR_2) and Carniolan (BR_3)), the time spent in plateau (TSP; mean: 118 day, 98 to 180 days), feed of autumn and spring (FAS; kg), working period in apiculture during year (WPA; mean:64 day, 0 to 180 days), frequency of changing queen (FCQ; mean:2 number/year, 1 to 5 number/year), and controlling beehives in summer (CFB; mean: 20 number/summer, 3 to 30 number/summer), respectively.

One-way ANOVA has been widely used in many fields (Eyduran et al., 2015a, b, c; Akin et al., 2016a, b) but it can give unreliable results in the violation of some assumptions. CART, CHAID and Exhaustive CHAID algorithms can be employed effectively for modeling nominal, ordinal and scale variables. CART algorithm permits ones to construct a decision tree structure on the basis of binary splitting criteria by partitioning a node into two child nodes, repeatedly (Akin et al., 2017; Duru et al., 2017; Eyduran et al., 2017). In the SPSS program, pruning option must be activated to remove needless nodes in the CART algorithm in contrast to CHAID and Exhaustive CHAID algorithms, which recursively construct multi splitting nodes until the variance within nodes will be minimum (Eyduran, 2016). Both CHAID algorithms performed for investigating the curve-linear and interaction relationships between independent variables estimate adjusted P values based on Bonferroni adjustment, and they convert scale variables into ordinal variables (Ali et al., 2015; Orhan et al., 2016). Minimum numbers of beekeeping farms in parent and child nodes were set at 8 and 4 in order to achieve the best predictive performance of the algorithms in AHY. Since AHY was a scale (continuous) variable, the algorithm employed F test for significance control of the effective independent variables in the CHAID algorithms. As a type of ANNs, multilayer perceptron (MLP) (also recognized as a feed-forward neural network), was used based on training (80%) and testing (20%) data sets. In MLP, input, hidden and output layers are available (Ali et al., 2015).

As a-nonparametric regression method, MARS (Multivariate Adaptive Regression Splines) is a data mining algorithm that permits to use piecewise basis functions for identifying a response variable and a set of input variables, and the MARS automatically determines knot locations. Prediction equation obtained by the MARS algorithm can be written as follows:

Where, βo and βm are the basis function parameters of the MARS algorithm specified based on the least squares criterion. The spline basis function βm (x) can be used as follows:

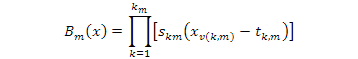
Where, km is defined as the number of knots, Skm takes either 1 or -1 and presents the right/left regions of the related step function, v (k,m) is the label of the input variable and tk, m is defined as the knot location.

The generalized cross validation (GCV) is approved to eliminate the redundant basis functions:

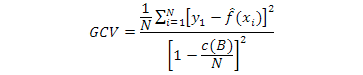
Where, N is the number of data and c (B) is a complexity penalty increasing with the number of basis function in the model.

As known, all the algorithms especially CART, CHAID and MARS included here contain significant variables. Information is available on significant predictors in the article. Things that are important for researchers are to determine the effect of predictors on dependent variable and to reveal interaction effects of significant predictors on dependent variable. In the case of ANNs, sensitivity analysis and have been made. Minimum RMSE and SD ratio values have been obtained. In MARS modeling, we obtained the lowest (Generalized Cross-Validation) GCV. The lower GCV, the better MARS is in the predictive performance. Also, number of terms was set for producing the predictive performance to explain it at the highest ratio of variability of dependent variable.

In the statistical modeling of the survey, CHAID, Exhaustive CHAID, CART, MARS algorithms and MLP, a type of ANN, were compared in terms of their predictive performance in AHY as described by Ali et al. (2015) and Nisbet et al. (2009). Model evaluation criteria estimated in their performance comparison are illustrated below:

Coefficient of Determination (%):

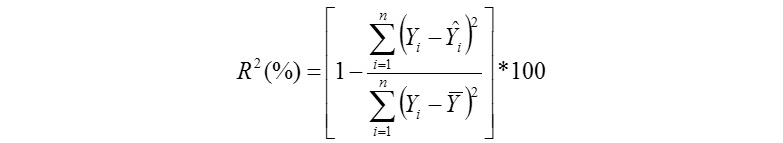
Adjusted Coefficient of Determination (%):

Adj%20COD.jpg

Coefficient of Variation (%):

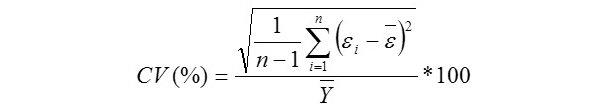
Standard Deviation Ratio:

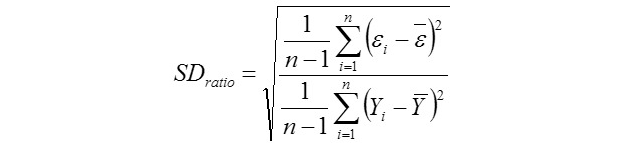
SD%20ratio.jpg

Relative Approximation Error (RAE):

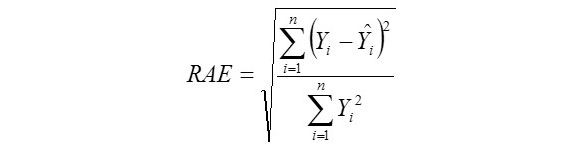
Root Mean Square Error:

Where, Yi is the actual AHY value of ith beekeeping farm, Ῡi is the predicted AHY value of ith beekeeping farm, Ῡ is mean of the actual AHY values of beekeeping farms, ɛi is the residual value of ith beekeeping farm, έ is mean of the residual values, k is number of independent variables found significantly in the model, and n: total sample size. But, k is number of terms in only the MARS modeling. The residual value for each beekeeping farm can be calculated via ɛi = Yi - Ῡi. The Pearson correlation coefficients between the actual (observed) and predicted AHY values were also calculated for each of the data mining algorithms evaluated in the survey (Karadas et al., 2017).

We reported the highest performances obtained for all the models in the study having a sample size of 85 enterprises. It is extremely difficult to construct the suitable tree structure for 80% training and 20% testing subsets in the limited sample size for the first three algorithms. In this regard, a cross validation of 10 for CART, CHAID, Exhaustive CHAID and MARS algorithms has been adopted. In the 10-fold cross-validation, the whole data set (85 records) was randomly allocated into 8 approx. equal parts of 8 records, from which nine were used to train a given type of a prediction model and one served as an independent test set. This procedure was repeated 10 times. Consequently, each part of the original data set was used as a test set exactly once and each of the 10 iterations produced a separate prediction model. In the IBM SPSS v. 23 programs, 80% training and 20% testing subsets can be only specified for ANNs. Minimum enterprise numbers for parent and child nodes were set 8 and 4 for CART, CHAID, Exhaustive CHAID algorithms with the aim of obtaining their best predictive performances. Results of all the algorithms have been obtained at the best predictive levels (the highest r, R2(%), Adj. R2(%), and the lowest CV(%), SDratio, RAE and RMSE).

Multilayer perceptron algorithm (that can be specified in the IBM SPSS 23 ver. software) has been used as a type of ANNs to obtain the best neural network as also reported in material and methods of the present study. Significant predictors in MLP after sensitivity analysis were considered. R2 is generally considered as a square of the correlation coefficient between actual and predicted dependent variable values. R2 and Adjusted R2 formulas are currently available in the current MS. I considered roughly 30 networks on the basis of minimal RMSE and SD ratio. Number of hidden layer is one. Number of units in hidden layer is three. Hyperbolic tangent was used as an activation function for output layer. Epoch number is reached when the estimation process is obtained.

To obtain the lowest GCV value in the MARS algorithm, we considered that initial maximal number of basis functions was 100 and that number of interaction degree was four. Afterwards, we finally made some specifications for the best predictive accuracy as: number of terms: 17, number of basis functions: 34, order of interactions: 4 and Prune: Yes.

The best algorithm should have the highest r, R2(%), Adj. R2(%), and the lowest CV(%), SDratio, RAE and RMSE (Ali et al. 2015). See the chapter “Examples of the use of data mining methods in animal breeding” written by Grzesiak and Zaborski (2012) for more detailed information on model evaluation criteria.

MARS analysis was performed using STATISTICA 8.0 trial version. Other algorithms were analyzed through IBM SPSS ver. 23.

Results and Discussion

We have primarily documented the comparison of three data mining algorithms in the prediction of AHY by means of some independent variables reported in materials and methods section. Results of model evaluation criteria for three data mining algorithms are given in Table I. Predictive performance of the MARS algorithm was found more advantageous in model evaluation criteria than other algorithms. The finding on the understandability of the data mining algorithms was also informed by some authors, who worked in animal science fields (Eyduran et al., 2013; Yilmaz et al., 2013; Khan et al., 2014; Ali et al., 2015).

Results of the decision tree diagram constructed by the Exhaustive CHAID algorithm used to determine factors affecting average honey yield per beehive (AHY) are depicted in Figure 1. Amongst the factors examined in the survey, number of full beehives (NFB), working period in apiculture during year (WPA, day) and control frequency of beehives in summer (CFB) were ascertained to be significant factors in regression tree diagram. Coefficient of determination predicted for the Exhaustive CHAID algorithm was estimated as 63%. Average honey yield per beehive for Node 0 was found 9.777 (S=4.568) kg for 85 beekeeping farms in the survey data, which was lower than the AHY amounts found by Korkmaz and Kumova (2000) (15.39 kg) in Adana and Icel province of Turkey, by Castellenos-Potenciano et al. (2015) (28.9 kg) in the Gulf of Mexico, by Cejvanovic et al. (2011) (13.53 kg) in the Bosnia and Hercegovina, by Marinkovic and Nedic (2010) (11-21 kg) in various districts of Serbia, as a result of different climate conditions, managerial systems, plant flora and various bee breeds etc. But, usage of data mining algorithms for modeling honey production with the goal of finding out effective independent variables is unavailable in apicultural data. In this regard, the present survey is the first report for application of data mining algorithms.

Table I.- Results of model assessment criteria for the data mining algorithms.

Algorithm	R2 (%)	Adj.R2 (%)	CV (%)	SDratio	RAE	RMSE	R
Exh. CHAID	61.50	60.40	28.80	0.610	0.200	2.800	0.786b
CHAID	58.79	57.27	29.86	0.639	0.270	2.900	0.769b
CART	55.02	53.75	31.20	0.667	0.280	3.030	0.744b
GLM	55.01	43.60	35.09	0.671	0.283	3.050	0.742b
ANN	78.32	75.90	21.62	0.463	0.181	2.105	0.885ab
MARS	83.31	79.08	19.08	0.408	0.170	1.855	0.913a

a,b, difference between r values with different letter was significant (P<0.01).

In the survey, Node 0 was partitioned into four child nodes (Nodes 1, 2, 3 and 4) according to NFB, respectively (Adj. P value=0.000, F=12.521, df1=3 and df2=81). Node 1 was the first subgroup of beekeeping farms with NFB < 38. Node 2 was the second subgroup of those with 38 < NFB < 60. Node 3 was a terminal node which is the third subgroup of those with 60 < NFB < 70. Node 4 was the fourth subgroup of those with NFB > 70. Average AHY values for Nodes 1-4 were 14.156 (S=5.458), 9.855 (S=4.019), 5.599 (S=1.472) and 8.239 (S=2.628) kg, respectively.

The effect of WPA on AHY of Nodes 1, 2 and 4 was significant. Node 1 was split into two new child and terminal nodes (Nodes 5 and 6), respectively. Node 5 was the fifth subgroup of those with NFB < 38 and WPA < 112. However, Node 6, the sixth subgroup of those with NFB < 38 and WPA > 112, produced the highest AHY among other Nodes. The significant difference between AHY averages of Nodes 5 and 6 was determined (10.792 (S=4.835) vs. 17.940 (S=3.234) kg), respectively.

Node 2 generated four nodes numbered 7, 8, 9 and 10 with respect to WPA, respectively. Node 7 was the seventh subgroup of those with 38 < NFB < 60 and WPA < 109.900. Node 8 was the eighth subgroup of those with 38 < NFB < 60 and 109.900 < WPA < 117.590. Node 9 was the ninth subgroup of those with 38 < NFB < 60 and 117.590 < WPA < 125.290. Node 10 was the tenth subgroup of those with 38 < NFB < 60 and WPA > 125.290. Average values in AHY for Nodes 7, 8, 9 and 10 were predicted to be 7.385 (S=2.081), 9.309 (S=4.926), 11.350 (S=2.666) and 14.868 (S=2.638) kg, respectively. Nodes 8, 9 and 10 were terminal nodes, but CFB partitioned Node 7 into two child nodes (13 and 14) with the AHY averages of 6.100 (S=1.575) and 8.486 (S=1.878) kg, respectively. There was a significant difference in AHY between Nodes 13 (the thirteenth subgroup of those with 38 < NFB < 60, WPA < 109.900 and CFB < 4) and Node 14 (38 < NFB < 60, WPA < 109.900 and CFB>4), (Adj. P=0.032, F=6.027, df=1 and df2=11).

Node 4 was divided into child and terminal Nodes 11 and 12 in respect to WPA, with the AHY averages of 4.485 (S=1.891) kg and 9.029(S=2.014) kg, respectively. Node 11 was found statistically lower in AHY than Node 12. Node 11 was the eleventh subgroup of those with NFB >70 and WPA < 108.580. But, Node 12 was the twelfth subgroup of those with NFB >70 and WPA > 108.580.

The decision tree diagram constructed by the CART algorithm is given in Figure 2. In the CART algorithm, only NFB, WPA and AB independent variables were found significantly. Node 4 in CART’s tree diagram gave the highest AHY (16.298) for beekeeping enterprises with NFB < 44.00 and WPA > 118.140.

MARS data mining algorithm had higher predictive performance in the AHY prediction when compared to other algorithms. In the AHY prediction, other predictors with the exception of BR were included in the MARS prediction model given below:

AHY = 7.955 + 0.132*max(0; 54-NFB) + 0.008*max(0; FAS-300) + 0.0239*max(0; 300-FAS) – 0.00099*max(0; FAS-400)*max(0; 124.19-WPA) – 0.00163*max(0; 400-FAS)*max(0; 124.19-WPA) + 0.3429*max(0; WPA-124.19)*max(0; EL_6) – 3.51635*max(0; EL_2) + 0.00044*max(0; AB-49)*max(0; 54-NFB)*max(0; CFB-3) + 0.00056*max(0; 49-AB)*max(0; 54-NFB)*max(0; CFB-3) + 0.00004*max(0; 400-FAS)*max(0; 124.19-WPA)*max(0; CFB-3) – 0.00002*max(0; AB-49)*max(0; 90-TSP)*max(0; 300-FAS) – 0.262*max(0; WPA-124.19)*max(0; FCQ_3) – 0.0000007*max(0; AB-49)*max(0; 54-NFB)*max(0; 90-TSP)*max(0; 300-FAS) + 6.825*max(0; FCQ_1) – 0.239*max(0; CFB-3)*max(0; FCQ_1) – 0.00134*max(0; TSP-90)*max(0; 300-FAS)*max(0; EL_5)

If NFB < 54 then max (0; 54-NFB)=0. When NFB = 52, max (0; 54-52)=2. If you specified EL=2 as an ordinal variable in the MARS model, max (0; EL_5)=0 but only max(0; EL_2)=1.

If a specification was considered for FCQ=2 and EL=5, we can converted the model mentioned above into the following MARS model:

AHY = 7.955 + 0.132*max(0; 54-NFB) + 0.008*max(0; FAS-300) + 0.0239*max(0; 300-FAS) – 0.00099*max(0; FAS-400)*max(0; 124.19-WPA) – 0.00163*max(0; 400-FAS)*max(0; 124.19-WPA) + 0.00044*max(0; AB-49)*max(0; 54-NFB)*max(0; CFB-3) + 0.00056*max(0; 49-AB)*max(0; 54-NFB)*max(0; CFB-3) + 0.00004*max(0; 400-FAS)*max(0; 124.19-WPA)*max(0; CFB-3) – 0.00002*max(0; AB-49)*max(0; 90-TSP)*max(0; 300-FAS) – 0.0000007*max(0; AB-49)*max(0; 54-NFB)*max(0; 90-TSP)*max(0; 300-FAS) – 0.00134*max(0; TSP-90)*max(0; 300-FAS)*max(0; EL_5)

When we have NFB=60, FAS=400, WPA=114.3, EL=5, AB=42, CFB=3, TSP=60 and FCQ=1, we predicted AHY = 14.788 kg through the first MARS model.

The results of present survey could not be discussed with earlier results due to the differentness of sample size, the used variables, their interactions, climate condition, and more especially statistical analysis methods. To our knowledge, because we have initially measured statistical performance of CART, CHAID, and Exhaustive CHAID data mining algorithms in order to predict AHY from independent variables considered in the survey. Any statistical assumption of the distribution of independent variables was not required for the algorithms, which have a vital role in the classification of those showing similar tendency in AHY. Afterwards, MARS prediction model developed for the first time in literature will present a novel approach for further similar studies.

Conclusions

Beekeeping is very important for small scale farms that are willing to obtain extra income and livelihood in honey production. In this study, predictive performances of several data mining algorithms (CART, CHAID, Exhaustive CHAID and MARS) and artificial neural network algorithm (Multilayer Perceptron, MLP) were measured comparatively. In the Exhaustive CHAID, only 3 independent variables such as NFB, WPA and CFB were found statistically. In the CART algorithm, NFB, WPA and AB independent variables were found to be significant. In the MARS algorithm, significant main and interaction effects of NFB, FAS, WPA, EL, AB, FCQ and TSP were detected. The significant order of the Pearson coefficients between actual and fitted values in AHY was MARS (0.913a) > ANN (0.885ab) > Exhaustive CHAID (0.786b) > CHAID (0.769b) > CART (0.744), (P<0.01).

It was concluded that the MARS algorithm more informative with the best predictive accuracy might offer a good solution to beekeepers in revealing interactions of significant independent variables.

Statement of conflict of interest

Authors have declared no conflict of interest.

References

Akin, M., Eyduran, S.P., Ercisli, S., Yilmaz, I. and Cakir, O., 2016a. Phytochemical profiles of wild grown blackberry and mulberry in Turkey. Acta Sci. Pol. Hortorum Cultus, 15: 3-12.

Akin, M., Eyduran, S.P., Ercisli, S., Kapchina-Toteva, V. and Eyduran, E., 2016b. Phytochemical profiles of wild blackberries, black and white mulberries from southern Bulgaria. Biotech. biotechnol. Equip., 30: 899-906. https://doi.org/10.1080/13102818.2016.1204943

Akin, M., Eyduran, E. and Reed, B.M., 2017. Use of RSM and CHAID data mining algorithm for predicting mineral nutrition of hazelnut. Pl. Cell Tissue Organ Cult., 128: 303-316. https://doi.org/10.1007/s11240-016-1110-6

Ali, M., Eyduran, E., Tariq, M.M., Tirink, C., Abbas, F., Bajwa, M.A., Baloch, M.H., Nizamani, A.H., Waheed, A., Awan, M.A., Shah, S.H., Ahmad, Z. and Jan, S., 2015. Comparison of artificial neural network and decision tree algorithms used for predicting live weight at post weaning period from some biometrical characteristics in Harnai sheep. Pakistan J. Zool., 47: 1579-1585.

Castellanos-Potenciano, B.P., Gallardo-Lopez, F., Díaz-Padilla, G., Perez-Vazquez, A., Landeros-Sanchez, C. and Sol-Sanchez, A., 2015. Apiculture in the humid tropics: socio-economic stratification and beekeeper production technology along the Gulf of Mexico. Glob. Sci. Res. J., 3: 321-329.

Cejvanovic, F., Grgic, Z., Maksimovic, A. and Bicanic, D., 2011. Assumptions of economic model for sustainable productions of beekeeping in the Bosnia and Hercegovin. J. agric. Sci. Technol., 5: 481-485.

Duru, M., Duru, A., Karadas, K., Eyduran, E., Cinli, H. and Tariq, M.M., 2017. Effect of carrot (Daucus carota) leaf powder on external and ınternal egg characteristics of hy-line white laying hens. Pakistan J. Zool., 49: 125-132. https://doi.org/10.17582/journal.pjz/2017.49.1.125.132

Erkan, C. and Askin, Y., 2001. The structure and activities of beekeeping in Bahçesaray, Van Yuzuncu Yil University, Agricultural Faculty. J. agric. Sci., 11: 19-28.

Eyduran, E., Yilmaz, I., Kaygisiz, A. and Aktas, Z.M., 2013. An investigation on relationship between lactation milk yield, somatic cell count and udder traits in first lactation Turkish Saanen goat using different statistical techniques. J. Anim. Pl. Sci., 23: 731-735.