Research Article

Estimation of Farm Level Technical Efficiency in Maize Production at the High Mountain North Region of Pakistan

Arif Alam1*, Faridullah2, Ikram Shah1, Shahzad Khan3, Noor Elahi1 and Ehsan Inamullah1

1Department of Development Studies, COMSATS University, Islamabad, Abbottabad Campus, Pakistan; 2Department of Environmental Sciences, COMSATS University Islamabad, Abbottabad Campus, Pakistan; 3Institute of Development Studies, The University of Agriculture, Peshawar, Pakistan.

Received | December 24, 2019; Accepted | September 28, 2020; Published | October 14, 2020

*Correspondence | Arif Alam, Department of Development Studies, COMSATS University Islamabad, Abbottabad Campus, Pakistan; Email: arifalam@cuiatd.edu.pk

Citation | Alam, A., Faridullah, I. Shah, S. Khan, N. Elahi and E. Inamullah. 2020. Estimation of farm level technical efficiency in maize production at the high mountain north region of Pakistan. Sarhad Journal of Agriculture, 36(4): 1054-1062.

DOI | http://dx.doi.org/10.17582/journal.sja/2020/36.4.1054.1062

Keywords | Stochastic frontier analysis, Technical efficiency, Maize production, High mountains of Pakistan, Farm inputs

Introduction

Pakistan is an agricultural country, having a parched atmosphere in nearly two-thirds of its territories. Climatic fluctuation has an immediate and unfavorable effect on the sustenance and improvement, particularly in dry ranges. Among climatic elements, precipitation has a tremendous impact on the production of crops (Khuram and Ghulam, 2011). Agriculture in Pakistan relies on water obtained from precipitation and snowmelt. Pakistan confronts the issues of floods, drier seasons, and inadequate water for crop production. Irrigation water availability predominantly relies on climatic variable, for example, air temperature, sunlight-based radiation, relative moisture, wind speed and agronomic components like phases of the crop (Ghazala and Mahmood, 2009).

In Pakistan, maize stands third most essential cereal crop after wheat and rice respectively. It is not just consumed as nourishment grain, but also utilized as a forage crop for livestock. Being a commercial/industrial crop, it is also an ingridient for several items that are produced from grains. Maize grain holds about 1.7% ash, 3.0% sugar, 5.8% fiber, 4.8% oil, 10% protein and 72% starch (Chaudhary, 1993). The annual grain crop production in Pakistan amounts to 2.96 million tons, with an average yield of 2,893 kg/ha on an area of 1.02 million hectares (GOP, 2007). While the area under maize crop was 1.06 million hectares in 2008, total production was 3.31 million tonnes, with an average yield of 3264 kg/ha (GOP, 2008). It accounts for 8.5% of the total cereal cropped area, makes a 2.1% contribution to the value addition in the agriculture sector and contributes 0.4% to the national GDP (Bashir et al., 2010).

The cultivation of maize and its multiple uses for domestic, commercial and industrial purposes play a critical economic role in Pakistan by generating income and employment across its entire value chain. Maize is considered an ideal vehicle for pro-vitamin (A) enhancement and delivery in areas with limited access to supplements and fortified foods (Baryan at el., 2014). Land of Pakistan is considered very favorable for maize production, however, while comparing with other maize growing countries, its yield per hectare is still very low (Tahir et al., 2011). Potential of maize crop is very high in terms of returns and its swift responses to different agronomic practices. However, numerous limitations hinder its yield, i.e. imbalanced utilization of fertilizers, customary sowing techniques. Life cycle of maize crop is highly responsive to water avaiability. At any phonological stage i.e. vegetative, regenerative and development stages, the shortage of water shows a diverse reaction with effect on grain yield (Cakir, 2004).

Gilgit-Baltistan (GB)’s economy is mostly based on subsistence crop production. The ecosystem of the mountain region is fragile and tends to be relatively low productive (Ahmed, 2001). However, in GB, maize crop is limited to lowlands and highly influenced by irrigation water availability. It is cultivated mainly in the season of Kharif (summer), although in some parts of Gilgit, Ghizer, Skardu, Diamer and Astore districts, it is grown as a crop of Rabi (winter) in single cropping zones mainly as a fodder crop. Maize is also an essential diet component in the wintertime. Moreover, the maize stover is utilized by livestock. The cultivation of maize usually starts in the middle of June and ends in the middle of July in double cropping zones. Harvesting begins in the third week of September and continues to the first week of November. Yields are 2,400, 1,600 and 1,800 kg/ha for the low, middle and high-altitude regions respectively (Scott, 2003). These yields are much lower than the national average yield, which is pointedly below the potential of the region. A slight reduction in productivity can be seen with the rise in altitude. This difference in productivity could be attributed to poor fertility of soil, low temperatures, and short growing seasons at high altitude areas like Astore, Yasin, Khyber, and Skardu (Khan et al., 2006). The existing crop rotation indicates that there are significant chances of increase in productivity, in the given zone and location. However, to meet consumption demands, farmers are motivated to harvest maize even having low productivity.

Depending on topography and soil type, the optimum population of plants, proper seed bed preparation, weeds control, timely control of pests and diseases, efficient utilization of fertilizer and proper irrigation can play a pivotal role in the improvement of maize productivity. Also, factors like use of local seed varieties and self-stored seeds, and inadequate use of inputs, lack of storage arrangements, lack of awareness regarding improved seeds, and lack of awareness of modern techniques constrain maize yield. Accordingly, in the mountainous region of Pakistan, one of the key elements to improve maize productivity is to enhance the technical efficiency of farms.

Elibariki et al. (2008) also argued that improved inputs and technological innovation is not the only way to increase the productivity, in fact, it also depends upon well-organized use of farmers’ skills and resources. Alam et al. (2012) also found that technical efficiency of potato and vegetable growers can be increased by enhancing their skills and knowledge, through the use of an appropriate amount of inputs and proper utilization of irrigation water in GB. Specifically, there is a paucity of information regarding factors influencing maize productivity in GB. Therefore, the current study is timely to be carried out to highlight all the above mentioned opportunities and constraints. The result of this study will be helpful for maize growers for improving their production efficiency. Therefore, this study attempts to bridge the knowledge gap by estimating maize farm’s technical efficiency (TE).

Research objectives

Thus, the main objective of this study was to identify the opportunities for enhancing productivity by improving the technical efficiency of maize, and to determine the factors influencing maize production in the high mountain regions of Pakistan.

 

Materials and Methods

Study area and sampling

Two villages Phaker from Nagar District and Murtazaabad from Hunza District were selected for the purpose of data collection for this study. Both areas were selected purposely due to the reason that these areas are considered important maize production zones in the surroundings of major districts. Systematic random sampling technique was deployed, which was drawn from lists acquired from concerned offices. Approximately 112 farmers (including 52 from Phaker, 60 from Murtazaabad) were selected for data collection regarding maize crop during its cropping season.

Data collection

For primary data, a well-structured, comprehensive and pilot-tested interview schedule was designed. It ensured acquisition of in-depth information on numerous aspects of maize production. In person interviews with household heads formed the basis of data collection. Information regarding last one year was gathered from the respondents, as there was no or little-documented evidence available. Information collected regarding crop production, inputs and outputs etc. was aggregated in monetary terms and utilized for productivity analysis. Data regarding farm inputs comprised of fertilizers, seeds, machinery, labor and irrigation information, whereas, data regarding farm outputs included information on gross production. Socio-economic characteristics of the farmers were also gathered which included age, literacy level, household size, farm size, locality of farmland, soil quality, source of credit, farming experience, and farmers knowledge regarding climatic effects etc. Although an overwhelming number of households grew a variety of crops in the study area, i.e. potatoes, fodder, wheat, vegetables and maize (in single cropping zones), this study, however, focused on maize crop.

Total production of maize crop (assessed in Pak Rupees “Rs”) was the dependent variable of this study. Crop inputs considered were fertilizers, agrochemicals, own seeds, purchased (hybrid) seeds and hired labor, the cost of mechanization and the frequency of irrigation applied. These variables were expressed in terms of their aggregate values. This method was used in order to cover for the paucity of crop data per unit area (kg per kanal), especially in case of agrochemicals. Hired labor was measured monetary value again because of the absence of data per person, since labor hiring follows a contractual mechanism. Wages of family labor was not included in the study as most of the agriculture activities are of subsistence level. The cost of machinery was taken from the monetary value of machine rents, on the basis of per hour work of ploughing and threshing. Farmers were only equipped with traditional cultivation tools, not larger machineries like tractors, threshers etc.

Theoretical and analytical framework

Productive efficiency can be improved by developing innovative production technologies and by adopting these techniques. The two popular and widely used methods for productivity estimation are Stochastic Frontier Analysis (SFA) and Data Envelopment Analysis (DEA), which are suitable for estimating the level of productive efficiency and also for identifying its determinants. To assess the technical efficiency of any production system, SFA is widely used. It can be used with multi-inputs and one output. On the other hand, DEA focuses on multiple-input and multiple-outputs technologies of production by using a mathematical programming method or non-parametric approach.

In this study, to assess the Technical Efficiency (TE) of maize production by the individual farms, stochastic frontier production function was applied. The SFA has some advantages. According to Coelli and Battese (1996), SFA is more preferable than DEA with respect to agricultural production. Data can be influenced by two-sided measurement errors, particularly in the developing countries. Pest attacks, disease, weather conditions and one-sided component are the additional effects, these are possible factors that can lead to inefficiency. As a result, SFA developed by Aigner et al. (1977) was considered suitable for this study.

Cobb-Douglas and translog stochastic production frontiers were used to determine the influence of input and socio economic factors on efficiency and productivity. Translog function was also used by Rahman and Hasan (2008) and Wilson et al. (2001) to assess the technical efficiency of crops. On the basis of the geometric mean of the sample, translog function delivers second-order approximation to the technology. However, the reason for using Cobb-Douglas function is well known and extensively reported in the literature.

The stochastic production frontier of Cobb-Douglas is:

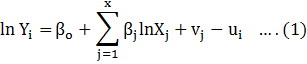
The translog model, in contrast to Cobb-Douglas function, has been produced and is given as:

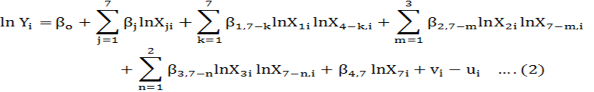
Where ln denotes natural logarithm and Yi represents gross production of maize in PKRs of the ith farm. β0 represents the intercept, whereas, β1-7depicts parameters of responses to be valued or elasticities corresponding to each input (i=1,2,3,…7). X1 is hired labor cost in Rs/kanal. Fertilizer cost is X2 in Rs/kanal, X3 reflects agrochemical cost in Rs/kanal, X4 is own seeds in Rs/kanal, X5 is purchased seeds Rs/kanal, machinery cost with service cost is in Rs/kanal and X7 is irrigation applied in numbers for maize crop. While, in the second order level of translog frontier model, j,k,m and n denote the interaction between the seven inputs. Further, it is also possible to represent the interaction between various inputs in production.

Vi depicts two-sided error component and reveals random variations in output as a result of factors outside the control of the farmers. On other hand, it also displays the measurement error effects in the output variable and other statistic noise. Assuming it to be normally distributed with zero mean-variance σ2, v and ui is a non-negative random variable associated with technical inefficiency (TIE). Production assumed to be independently and identically distributed (at zero) of the normal distribution with mean μi and variance σ2, u. While μi is defined by:

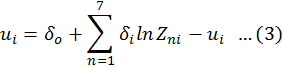
In above equation μi denotes effects of inefficiency, δ0 shows the intercept term and δ1-7 represents a parameter for the ith explanatory variable. Z1 denotes farm size in kanals; Z2 shows age of farmers in years; Z3represents literacy level of the farmers in terms of (number of years in school); Z4 indicates household size (number of persons in household); Z5represnt the locality of farmers (altitude/ elevation of the farmland); Z6 shows soil quality (if the quality of soil is good=1, otherwise 0); Z7 is a dummy variable for the villages, (if the respondents is from Phaker =1, otherwise 0).

The Maximum Likelihood Estimates (MLE) is defined by equations 1, 2 and 3for all parameters of the stochastic frontier production and inefficiency model, which was applied for estimation by using the program FRONTIER 4.1 (Coelli, 1996). It also estimated the variance parameters in terms of parameterization as:

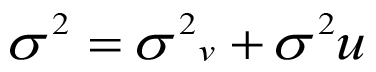….(4)

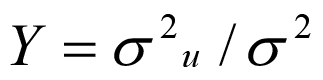…(5)

So that 0≤ γ ≥1: The γ value ranges from 0 to 1 the values close to 1 representing that random component of the inefficiency effects has a significant contribution to the analysis of the production system. The technical efficiency of production of the ith farmer (TEi) given the levels of inputs used is defined by:

TEi = exp (-Ui) …(6)

The TE of a farmer was between 0 and 1 and is inversely related to the level of the technical inefficiency effects (Battese and Coelli, 1995). The TE is also predicted using the FRONTIER 4.1 package, which calculates the ML estimate of the predictor for Equation 6 that is based on its conditional expectation, given the observed value of (Vi-Ui). If Ui is equal to 0, the production is on the frontier and the farm is technically efficient. If Ui is greater than 0, the production will lie below the frontier and the farm is technically inefficient (Coelli et al., 2005). The technical inefficiency can only be estimated if the inefficiency effects are stochastic and have a particular distribution specification (Battese and Coelli, 1995).

Statistical analysis

Key variables analyzed in this section have already been defined and summarized in the previous sections, under the econometric model. The values are described on the basis of per unit. Models were estimated by using multiple regression models through Ordinary Least Square (OLS) estimation procedures. Multiple regressions were applied, based on linear combinations of interval, dichotomous, or dummy independent variables, to determine (predict) variance in an interval scale. To assess the parameters of the MLE and stochastic frontier production function was frequently in use. On the other hand, Coelli (1995) concludes that the maximum likelihood estimator is asymptotically more efficient than the OLS estimator.

For frontier model in logarithm form, regression accounted for all independent variables along with dependent variables. However, the indicators of technical inefficiency are in absolute values; as this model is constituted by variables those may affect technical efficiency and the resultant household decisions. Most commonly used forms in empirical studies are Cobb-Douglas and Translog production functions. However, Translog or flexible functional method causes severe difficulty of multicollinearity, whereas, Cobb-Douglas function is not difficult to estimate, interpret and this is commonly used to determine technical inefficiency. Therefore, for the present study, Cobb Douglas form was used for estimation of inefficiency.

The parameters associated with σ2 and γ were used to evaluate the overall technical inefficiency effects. The estimate is significantly different at 1% for the variance parameters σ from zero. This indicates statistical confirmation of presumption made in this study, that there are differences in technical efficiency.

 

Results and Discussion

Results of descriptive analyses

The descriptive statistics of input and output variables related to production of maize (described in per unit basis) are presented in Table 1. The descriptive analysis shows that the average calculated value of yield per kanal was Rs. 10,492 for maize crop. The average cost for hired labor was Rs. 1,389, which makes the highest percentage amongother cost of inputs, followed by the cost of purchased seeds worth Rs. 1,227. It indicates that maize production requires more labor, while, the second highest cost of purchased seed indicates that farmers are trying to use improved varieties of seed for better productivity. However, fertilizer cost is in third place (Rs. 1,027). It reveals that spending more on input is not a guarantee for higher crop productivity.

In Table 2, the estimated parameters for MLE and OLS methods for the maize growing farmers are given. For maize growers’ data set, four MLE coefficients out of seven, of the inputs, are linked with outputs, which are different from zero and statistically significant. When parameters are measured based on OLS method, only two variables are significantly different. Compared to OLS method the MLE model provides are a better result. While the sign of a coefficient in the stochastic model directly represents the direction of the effect, it is also essential that the estimated parameters in the technical inefficiency model to show a negative sign, which implies a positive relationship. Existing market price in the study area was set to evaluate the inputs by quantities used as per kanal. The irrigation applied rate of each crop is taken as the frequency of irrigation delivered to the crops field and expected to have positive signs.

 

Table 1: Statistics of outputs and inputs and farm specific variables.

Variable name	Mean	S.D	Min	Max
Crop specific variables
Output Yi	10,492.7	2,344.4	4,480	18,615
Hired labor	1,389.4	388.6	650	2,850
Fertilizer	1,027.9	332.6	500	2,750
Agrochemical	970.3	548.6	555	3,090
Own seed	951.1	280.3	360	1,890
Purchased seed	1,227.3	493.1	111	3,600
Machinery cost	925.0	719.8	1,308	5,250
Irrigation numbers	22.6	2.5	16	30
Farm specific variables
Farm size (Kanal)	3.0	1.8	1.0	10.0
Age of HH (years)	58.5	9.2	38.0	74.0
Education level (years)	5.4	3.8	0.0	16.0
No. of household members	11.9	4.0	5.0	24.0
Loc. of farmers	0.6	0.5	0.0	1.0
Soil quality, (1= good, 0=others)	0.6	0.5	0.0	1.0
Dummy village	0.5	0.5	0.0	1.0

 

OLS and ML estimates of stochastic frontier analysis

Through means of output elasticities, parameters of Cobb-Douglas production function can be explained directly. As shown in Table 2, in MLE method, all the input parameters are statistically significant and have positive signs, excluding machinery cost. This indicates that these inputs are performing important roles in the production of maize. According to results, the maximum output elasticity was recorded as 0.27 for the cost of own seeds, followed by 0.19 for the purchased seeds. Both variables relate positively and are highly significant to maize productivity. These variables with higher elasticity are indicating that the total factor productivity contribution is dominant. It means that one percent increase in the usage of mentioned inputs would lead to a 27% and 19% rise in production of maize, respectively. Rise in output is the consequence of use of improved local varieties of seeds. On the other hand, plant population per area can be increased up torecommended levels by use of more purchased seeds in the field, to increase output/production.

 

Table 2: Ordinary Least Square (OLS) and Maximum Likelihood (ML) estimates of Maize.

Variables	OLS		MLE
	Coefficient	t-ratio	Coefficient	t-ratio
Stochastic frontier model
Constant	3.17	4.50***	2.88	4.72***
Hired labor	-0.40	-1.92*	0.11	1.20
Fertilizer	0.30	1.72	0.18	1.98*
Agrochemical	-0.13	-0.73	0.23	1.44
Own seed	0.53	3.07***	0.27	3.89***
Purchased seed	0.10	0.99	0.19	2.35**
Machinery cost	-0.04	-0.16	-0.15	-0.60
Irrigation numbers	-0.08	-0.29	0.09	0.190*
Technical inefficiency model
Constant			0.16	1.96**
Maize crop area (Kanal)			0.02	-2.24**
Age of HH (years)			-0.05	-2.48**
Education level (years)			-0.01	-2.29**
Family size (No.)			0.01	1.37
Location of farmers (altitude)			0.04	0.63
Soil quality (1= good, 0=others)			-0.00	-6.08***
Dummy village			-0.10	-0.86
Variance parameters
Sigma-squared (σ2)	0.29		0.45	5.75***
Gamma (γ)			0.87	90.63***
Ln Likelihood	86.25		107.08

Note: *** indicates significant at 1%; ** significant at 5% and * significant at 1%.

 

Other effective inputs for the maize production are irrigation water and fertilizer. Irrigation and fertilizer are significant inputs for the production of maize, as one percent increase in irrigation water and fertilizer usage leads to 18% and 9% increase in the output, respectively. Alam et al. (2011) reported that the use of improved irrigation system in GB region has beneficial effects for better land utilization and improved productivity, leading to higher farm income. Machine cost has a negative coefficient and is insignificant, as a result of small sized and irregular terraced fields, which typically takes more time to plough.

In MLE model, the estimates are significantly different for variance parameters σ2 and γ from zero. This implies statistical confirmation of presumption that there are differences in technical efficiency among farmers. The share of one-sided error in total variance (γ) is 0.87% of the two variances. This result indicates that the technical inefficiency effects are significant in the case of maize production.

Analyses of socio-economic and demographic variables

At the farm level, production efficiency is subjected to many socio-economic and demographic factors. In this study, some factors were found to be positively contributing towards enhancing efficiency of maize production, which includes: maize crop area (Kanal), age of HH (years), education level (years), family size (nos.), location of farmers (altitude), soil quality (1= good, 0=others), and a dummy for the village (Table 2).

It is evident that the farm size is significantly negative at 5% level of significance. It also implies that maize farmers operating small landholdings are technically efficient. Age, a proxy for farming experience, is expected to have a negative impact on technical inefficiency. Confirming this expectation, age of farmer is negative, and significant at 1%. It clearly indicates that older farmers are more efficient. Experience of older farmers’ leads to more efficient inputs utilization. Also, due to the more traditional and conservative nature of older farmers, cereal crops were preferred over cash crops. Moreover, numerous studies have also indicated age to have mixed impact on efficiency, depending upon crop type in the study area.

Education coefficient is also seen significantly negative implying that a higher level of education leads to higher TE, and this could be because of improved access to farm planning tools and information. However, the household size coefficient is positive but not significant, indicating large family memebers being less efficient than smaller ones. A dummy variable was used to identify the effect of technical efficiency on location (altitude). The insignificant and positive coefficient of dummy variable shows that it has no significant impact. Soil improvement investments surely lead to short and long-term economic benefits. Still, the interdependency between soil improvement and farm revenue in GB has not been studied. Research on soil quality is hence inevitable for this reason. Also, village dummy variable for vegetables and wheat was proved insignificantly negative (Alam et al., 2012)

Hypothesis test

Log-likelihood ratio test was employed to test the hypothesis on the validity and suitability of efficiency model. This test is defined as λ = –2 [Ln (H0) – Ln (H1)], where Ln (H0) and Ln (H1), where log likelihood values are attained from the running models (restricted/unrestricted respectively). Null hypothesis (i) identifies that effects of inefficiency were not stochastic. This was strongly rejected as per Table 3 results. Hypothesis rejection means that function for traditional mean response is not a suitable illustration for production function. Furthermore, the hypothesis of inefficiency effects being absent (i.e., γ = δ0 = δ1… δ7), are rejected at 5% significance level. This clarifies that an overwhelming number ofthe farmers work lower than technically efficient frontier, which was output oriented. In error component, there is no farmer specific or constant effect, as it is clearly shown in the third hypothesis test. As shown from the result, null hypothesis inclusion is rejected. Fourth hypothesis test implies collective significance of the inefficiency determinants. It rejects null hypothesis and indicates that explanatory variables influence farm efficiency collectively. However, it may not be individually significant.

 

Table 3: Likelihood ratio tests for maize.

Null hypothesis	Log likelihood	LR statistics	Critical value	Decision
Ho:γ = 0	107.08	29.08	14.07	RejectH0
Ho:γ = δ0 = δ1 …. δ7	117.20	49.38	25.5	RejectH0
Ho:= δ0 = δ1 …. δ7	84.13	19.84	12.59	RejectH0
Ho:= δ1 …. δ7	81.09	28.98	14.07	RejectH0

 

Technical efficiency analysis

Farm-specific technical efficiencies information is important for policy makers, as it provides a detailed overview of the nature of production and technology adopted at the farm level. Table 4 illustrates frequency distribution estimations of individual farms, and TE analysis. According to estimated efficiency scores, just 16% of farms are technically efficient above 80%.

 

Table 4: Frequency distribution of technical efficiency estimates.

Efficiency rating	Overall efficiency
	N	%
< 60	4	3.6
61-70	42	37.5
71-80	50	44.6
81-90	14	12.5
91-100	2	1.8
Mean efficiency	73.64
Minimum	58.61
Maximum	94.22

 

Overall, TE is estimated to be 73.6% (onaverage), and range between 58.6% and 94.2%. This implies that overall, farms are producing at an average of their 73.6% potential, given the state of technology and input levels. Therefore, it can be safely concluded that most of the farmers are severely constrained by technical inefficiencies as 27% of the technical potential is not realized. Therefore, there is a potential to improve productivity through efficient crop management without increasing current input levels.

 

Conclusions and Recommendations

The main aim of this study was to understand the opportunities for enhancing productivity by improving technical efficiency of maize crop and to determine the factors influencing maize production in high mountain regions of Pakistan.

Stochastic production frontier was used, accompanied by a model of technical inefficiency effects, to obtain information on production of maize crop in two villages. Crop production dynamics were assessed in terms of fertilizers, labor hired, seeds purchased, agrochemicals, cost of machinery and irrigation. As per obtained results, all these factors significantly impacted production of maize crop. Technical inefficiency model used explanatory variables like age of household head, size of household, farm size, literacy level, farmer location and type of soil etc. The results revealed that in high mountain regions of Pakistan, these variables affect TE positively with respect to production of maize crop.

Results regarding efficiency analysis revealed that farms on average reached 73% TE, and thus on average farmers are operating 27% below the potential output. However, TE is linked negatively with the size of the farm. Results also depict that maize growers were not only generating output below the potential level, but also working at a relatively lower level from the production frontier. This specifies that there is substantial room for improvement, relatively for the inefficient farms, to increase productivity/output. This can be accomplished by improving production efficiency and sustaining the efficiency of those operating closer to the frontier. It can also be illustrated from the results that longer experience of farming makes older farmers more efficient in growing maize crop. In this study, the determinants of TE analysis indicated that TE could be enhanced more effectively by farmers’ education, resulting in better uptake of modern production techniques and appropriate utilization of farm resources. Furthermore, establishing extension services on the basis of contemporary demands will improve farmers’ abilities towards the use of modern agricultural technologies.

 

Acknowledgements

Authors express their gratitude to the Higher Education Commission (HEC), Pakistan for funding this research project. Funding was provided by HEC under startup research grant program (SRGP) for assistant professors joining under IPFP/TTS.

 

Novelty Statement

The findings of the study may have a significant impact on the policies formulation about agricultural input and resources usage. This can be accomplished by improving production efficiency and sustaining the efficiency of those operating closer to frontier.

 

Author’s Contribution

Arif Alam: Main idea generator, write up of introduction, data collection, data analysis and overall write up.

Faridullah: Contributed in the write up of introduction and research methods and improved language.

lkram Shah: Contributed in the preparation of questionnaire and research methods.

Shahzad Khan: Contributed in the write up of literature review and research method and results.

Noor Elahi: Contributed in the preparation of questionnaire and research methods.

Ehsan Inamullah: Contributed in the write up of introduction and research methods and improved language of the manuscript.

Conflict of interest

The authors have declared no conflict of interest.

 

References

Ahmed, S., 2001. Background paper on water, northern areas conservation strategy, Gilgit, Pakistan. 64.

Aigner, D.K., C.K. Lovell and P. Schmidt. 1977. Formulation and estimation of stochastic frontier production function models. J. Econ., 6: 21-37. https://doi.org/10.1016/0304-4076(77)90052-5

Alam, A., H. Kobayashi, I. Matsumura and M. Esham. 2011. A comparative economic analysis of crop production between improved and traditional irrigation system: A case study of a village from Gilgit district in NAs of Pakistan. J. Rural Problem, 47(1): 132-137. https://doi.org/10.7310/arfe.47.132

Alam, A., H. Kobayashi, T. Matsuda, A. Ishida, I. Matsumura and M. Esham. 2012. Stochastic frontier approach to measure technical efficiency of two irrigation systems in Gilgit district, Gilgit-Baltistan region of Pakistan. J. Food, Agric. Environ., 10(1): 543-550.

Bashir, K.S., F. Ahmad and S. Sadaf. 2010. Crops area and production (by districts); (1981-82 to 2008-09). Government of Pakistan statistics division, federal bureau of statistics (Economic Wing), Vol. 1.

Battese, G.E. and T.J. Coelli. 1995. A model for technical inefficiency effects in the stochastic frontier production function for panel data. J. Empirical Econ., 20: 325-332. https://doi.org/10.1007/BF01205442

Cakir, R., 2004. Effect of water stress at different development stages on vegetative and reproductive growth of corn. Field Crops Res., 89: 1-16. https://doi.org/10.1016/j.fcr.2004.01.005

Chaudhary, A.R., 1993. Agronomy in maize Pakistan. Punjab agriculture coordination board, University of Agriculture Faisalabad, Pakistan.

Coelli, T.J., 1995. Recent developments in frontier modeling and efficiency measurement. Aust. J. Agric. Resour. Econ., 39(3): 219-245. https://doi.org/10.1111/j.1467-8489.1995.tb00552.x

Coelli, T.J., 1996. A guide to frontier version 4.1: A computer program for stochastic frontier production and cost function estimation. CEPA working paper 96/07 Department of Econometrics, University for New England, Armidale.

Coelli, T.J. and G.E. Battese. 1996. Identification of factors which influence the technical efficiency of indian farmers. Aust. J. Agric. Econ., 40(2): 103-128. https://doi.org/10.1111/j.1467-8489.1996.tb00558.x

Coelli, T.J., D.S.P. Rao, C.J. O’Donnell, G.E. Battese. 2005. An Introduction to Efficiency and Productivity Analysis. Second Edition. Springer. Pp 356.

Elibariki, E., S.H. Msuya and N. Tatsuhiko. 2008. Explaining productivity variation among smallholder maize farmers in Tanzania. Paper presented in XII World Congress of Rural Sociology of the International Rural Sociology Association, Goyang, Korea. MPRA Paper No. 14626. http://mpra.ub.uni-muenchen.de/14626/

Ghazala, N. and A. Mahmood. 2009. Water requirement for wheat crop in Pakistan. Pak. J. Meteorol., 6(11): 89-96.

GoP, 2007. Economic survey of Pakistan (2006-2007), Ministry of finance, Government of Pakistan, Pakistan.

GoP, 2008. Economic survey of Pakistan (2007-2008), Ministry of finance, Government of Pakistan, Pakistan.

Scott, P., 2003. Northern areas state of environment and development. Pakistan, Northern Areas Administration. IUCN Pakistan. pp. 290-303.

Baryan, G., C. Kaliwile, S.A. Arscott, S. Schmaelzle, S. Chileshe, N. Kalungwana, M. Mosonda, K. Pixley, C. Masi and S.A. Tanumihardjo. 2014. Biofortified orange maize is as efficacious as a vitamin A supplement in zambian children even in the presence of high liver reserves of vitamin A: A community-based, randomized placebo-controlled trial. Am. J. Clin. Nutr., 100(6): 1541-1550. https://doi.org/10.3945/ajcn.114.087379

Khan, S., H. Ashiq and Z. Shafiq. 2006. Overview of fodder crop production in Pakistan. A report submitted to PARC, Islamabad.

Khuram, R. and R. Ghulam. 2011. Rainfall variability and maize production over the Potohar Plateau of Pakistan. Pak. J. Meteorol., 8(15): 63-74.

Rahman, S. and M. Hasan. 2008. Impact of land fragmentation and resources ownership on productivity and efficiency: The case of rice producers in Bangladesh. Land use Policy, 26: 95-103. https://doi.org/10.1016/j.landusepol.2008.01.003

Tahir, M., S. Ghulam, A.N. Muhammad, N. Muhammad, W. Muhammad, M.R.J. Hafiz and R. Hasseb. 2011. The effect of intensity of tillage and herbicide application on spring planted maize (Zeamays L.) and its weeds. Pak. J. Life Soc. Sci., 9(2): 109-115.

Wilson, P., H. David and A. Carol. 2001. The influence of management characteristics on the technical efficiency of wheat farmers in eastern England. Agric. Econ., 24: 329-338. https://doi.org/10.1111/j.1574-0862.2001.tb00034.x