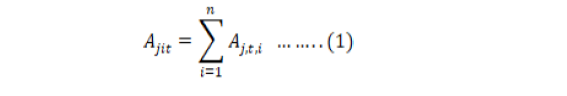Relationship between Climate and Year to Year Variability in Crop Yield: Selected Districts of Pakistan
Relationship between Climate and Year to Year Variability in Crop Yield: Selected Districts of Pakistan
Khush Bukhat Zahid1*, Ghaffar Ali2, Samina Sabir1 and Mohammad Fayaz2
1Kashmir Institute of Economics. University of Azad Jammu and Kashmir Muzaffarabad, Pakistan; 2Department of Agricultural and Applied Economics, The University of Agriculture, Peshawar, Khyber Pakhtunkhwa, Pakistan.
Abstract | This paper aims to test the impact of climate change on agricultural productivity of major crops, including rice, wheat and maize, in specific districts of Pakistan. This is done by observing year-to-year fluctuations in rainfall and temperature in relation to agricultural productivity for the period 1981-2009. For estimation purposes, the production function technique is used to evaluate the relationship between climate and yield variability. The results show that higher amount of rainfall has a negative and significant impact on the production of all crops including wheat, rice and maize. It may be because unexpected rainfall in Pakistan during monsoon season severely damages crops. This result is consistent with our expectation that high level of rainfall would decrease agricultural productivity and contribute to food insecurity in Pakistan. However, variation in temperature displays a stable trend and has significant positive impact on crop yield. This is contrary to our expectation that high temperature results in low agricultural productivity. This analysis is useful from the stand point of policy makers and analysts as it will help them develop policies relating to improvement in agricultural sector in the context of climate change.
Received | January 30, 2018; Accepted | November 22, 2018; Published | January 12, 2019
*Correspondence | Khush Bukhat Zahid, Kashmir Institute of Economics. University of Azad Jammu and Kashmir Muzaffarabad, Pakistan; Email: khushbukhatphd2009@gmail.com
Citation | Zahid, K.B., G. Ali, S. Sabir and M. Fayaz. 2019. Relationship between climate and year to year variability in crop yield: selected districts of Pakistan. Sarhad Journal of Agriculture, 35(1): 36-42.
DOI | http://dx.doi.org/10.17582/journal.sja/2019/35.1.36.42
Keywords | Climate change, Agriculture productivity, Temperature and rainfall, Production function technique, Yield variability
Introduction
In recent times, there has been a lot of focus on climate change and its impact on the different sectors. An overwhelming majority of scientists believe that climate change is real, and there is unequivocal scientific evidence to support that (SPORE, 2008). Climate change is characterized by a long-term change in average weather conditions of a certain region (IPCC, 2014). It is believed to be the most serious environmental threat posed to mankind, mainly due to its impact on agricultural productivity. It is observed that crops often respond negatively with a steep drop in net growth and yield when temperature exceeds the optimal level for biological processes. Developing countries seem to be most affected by this phenomenon largely due to the lack of knowledge and appropriate infrastructure needed to cope with the situation.
Scientific literature shows that in the coming decade, worldwide levels of precipitation and temperature are expected to increase, leading to poor agricultural growth. Evidence shows that changing climate has already affected crop yields in many countries, most commonly the developing economies where the livelihood of poor people largely depends on the agricultural sector (IPCC, 2014). This is particularly true due to the fact that there is absence of proper coping mechanisms, resulting in low adaptive capacities (SPORE, 2008; Apata et al., 2009). Pakistan, being a developing country, is also highly vulnerable to the damage caused by anomalies in climate. The flood of 2010 is a related example to support this argument. This flood was caused by heavy monsoon rains in said year, and led to heavy destruction of crops of wheat, maize, rice, and sugarcane.
Climate change and its impact on the agriculture sector has received high consideration in Pakistan because climate change is closely linked to two major issues faced by the Pakistan economy: food insecurity and poverty. The state of Pakistan as a developing country depends mainly on the agricultural sector, which is highly vulnerable to climate change. Agricultural activities and their allies are the largest sector, comprising 19.8 percent of GDP and providing employment opportunities for 42.3 percent of the country’s workforce. Agricultural growth rate has shown a downward trend in recent years (GoP, 2016).
Agriculture land is mostly located in arid and semi-arid zones, where temperature is usually higher than the global average. About 60 percent of the area receives less than 250 mm of rainfall per year, and 24 percent receives 250-500 mm rainfall annually (FRTFCC, 2010). Cereal yield is expected to decrease by up to 30 percent by 2050, along with the decline of gross water availability per capita for South Asia from 1820m3 in 2001 to 1140m3 in 2050 (IPCC, 2007). Agricultural practices are limited by weather; therefore, climate change is likely to affect the efficiency of the existing system of agricultural production, and in doing so, the fortune of related industries and the economy (White, 1985).
An open question is “how sensitive is inter-annual crop yield variability to climatic change?” Agriculture is a complex phenomenon which involves different biophysical processes and external factors such as technological progress, crop-climatic adaptation, CO2 concentration, and fertilization effects, among many other factors. These factors are difficult to model, but a current statistical answer can be obtained from historical records relating crop yield variability to climate. To address this, time-series and cross-sectional data are pooled for specific districts of Pakistan. This data includes climate variables in an approach much like that employed by Deschenes and Greenstone (2000; 2006) to measure inter-annual crop yield variability due to changes in climate. Previous studies used proxies for climatic data such as degree days and grid analysis but present study used actual annual data of temperature and precipitation without any modification from Metrological department of Pakistan and focus will be on the analysis at the district level to understand the relationship between climate and district level yield variability. In addition to this previous study used profit and total value of production as dependent variable but present study used yield for better interpretation of results. Data for yield variability in wheat, rice and maize is examined to see how they are affected by climate conditions. Least square panel data estimates of the impact of climate on year-to-year yield variability are constructed for the major agricultural crops along the lines of the stochastic production function approach.
This study is organized as follows: section two describes methodology. Section three provides elaboration of results and discussion. Section four concludes the finding of the study.
Materials and Methods
Nineteen districts were selected randomly from entire district wise map of Pakistan from different provinces and agro ecological zones based on data availability for the period of 1981-2009.
District level data on crop area and production is obtained from Statistics Division Federal Bureau of Statistics Government of Pakistan from 1981-82 to 2008-09. The unit of measurement in original data is thousand hectares for area and production in thousand tons which is then converted into yield in kilogram per hectare. Keeping in view the goals identified above, focus will be on the analysis at the district level to understand the relationship between climate and district level yield variability. For each crop, the total crop area and production in each district is summarized as:
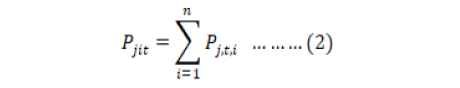
Where;
Ajit and Pjit are total area and production in each district respectively; of crop j in year t in district i. For each crop j yield was computed by dividing production by harvested area.
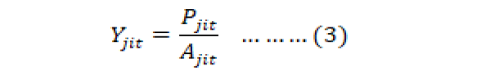
Over time changes in yield result not only from climate variations, but also from changes in management practices, such as the use of new technologies. Thus, an important step is to first account for technology trends when analyzing climate-yield relationships. Here time trend in linear trend model is incorporated to capture these effects. In order to see the impact of climatic variable on inter annual yield variability, district level time series data of climatic variables is taken which consider annual mean temperature in Celsius degree centigrade and the gauge of precipitation is millimeter. The data for precipitation and temperature are collected from Pakistan Meteorological Department.
Panel data model is used to explore the relationship between annual yield variability and climatic variables. First univariate unit root test is applied on each series of panel of districts. Consider ‘N’ cross sectional units observed over the time period ‘T’. Let ‘Yit’ be an annual yield variability and it can be written as first order autoregressive process.
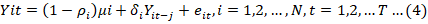
The δijs are lagged coefficients in the process of parameterizing ‘Yit’. Initial value of annual yield is given. Now subtract Yit-1 from both sides of Equation (1) and we write this as:
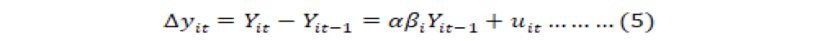
Where;
αi =(1- ρi) μi, βi = (1-δi). Im et al. (1997) proposed a test for unit root and null hypothesis of unit root which is stated as H0 : βi= 0 for all ‘i’ against the alternative hypothesis.
H1 : βi< 0 for i = 1, 2, ….N, βi = 0, for i = N1 + 1, N1+ 2,…,N through Dickey-Fuller (ADF) (1979) regression (2). This alternative specification of alternative hypothesis allows βi differing across district, group or cross sectional units. Moreover, it is more general than homogenous hypothesis β < 0.
Levin and Lin (1993) proposed unit root test based on the assumption that individual processes are cross-sectional independent. Consider the following equation to apply Levin and Lin (LL) test.
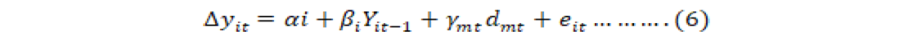
Where;
‘dmt’ is the deterministic variable--- We test the null hypothesis that H0 : βi = 0, for all i against alternative hypothesis H1 : βi = β<0, for all i with weak convergence to standardize normal variate as T and N approach to infinity and T/N approaches to zero.
Similarly, we tested unit root has been conducted in all given series by adopting the same methodology.
Production function for yield variability
Just and Pop (1978) stochastic production function is estimated to analyze the relationship between annual crop yield variability and independent variable. This production function has the advantage that it does not impose any dependency between any item’s effect on annual yield variability and its effect on mean yield variability (Chen et al., 2004). The following production function by Panel least square dummy variable method is estimated.
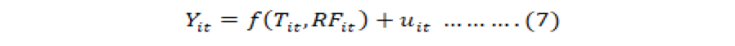
Where;
Yit is the annual yield, Tit is the annual average temperature, and RFit is the average annual rainfall. Uit is the random term, which is independently and identically distributed. Specifically, Cobb-Douglas production function is used to estimate the relationship between yield variability and its explanatory variables. It can be written as:

For linear transformation, take the natural logarithm on both side of the Equation (8).
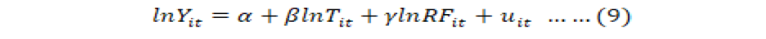
Input elasticities of production function are also calculated, which imply percentage change in annual yield variability due to one percent increase in temperature and rainfall variability. This equation is estimated using panel data techniques or methods.
Panel data model
Panel data set is used to gain information on seasonal effect of climate on seasonal yield variability of crops in selected districts of Pakistan. Difference in yield variability of individual crops is very small but there is a trend in seasonal yield variability and that is controlled by using technological change in our model which is captured by time trend. Panel data models capture the impact of omitted variable through time invariant fixed effect and random effect models. Fixed Effect Model (FEM) is specified as:
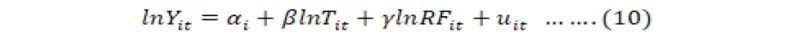
Where;
αi‘s are the unobserved district specific effects. This model is also known as one way error component model. This model is estimated by using least square dummy variable method. District specific dummies are used. FEM is based on assumption that unobserved effects are correlated with explanatory variables. Within and within group method are also used as alternative methods to estimate FEM.
On the other side, district specific and time effects are considered as random. This type of model is known as Random Effect Model (REM). It can be written as:
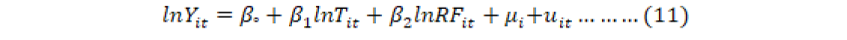
Where;
μi is unobserved random effects. REM relies on assumption that no relationship exists between random effect and explanatory variables. REM is estimated by using feasible generalized least square (FGLS) and maximum likelihood methods.
Hausman (1978) proposed a test to decide which technique is more appropriate for estimation. Null hypothesis of Hausman test states that unobserved effects are uncorrelated with explanatory variables i.e., E(βiXit)= 0. Null hypothesis implies that RE model is consistent against the alternative hypothesis that FEM is consistent. Hausman test statistic is formulated as:
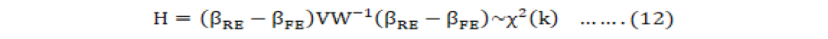
If H is significant, then we use fixed effect model for estimation.
Results and Discussion
Result of Im, Pesaran and Shin, Levin and Lin, and ADF Fisher Chi Square panel unit root test results are presented in Supplementary Table 1. The results reveal that all variables are stationary at level with intercept and trend except maize yield with intercept. These results clearly show that null hypothesis of panel unit root is rejected at various lags length. We rely on the results of IPS test which is applied for heterogeneous balanced panel. Although Levin Lin test is powerful when time period is large, it has a problem that it assumes a stationary for each series in whole panel. Another advantage of using IPS test is that it captures the region-specific effects (Pesaran and Tosetti, 2011). Moreover, ADF test is used for time series with limited number of observations, but in panel data the number of observations increases which make ADF test less powerful.
First, the random effect model with wheat yield as a dependent variable, and temperature, rain and time trend as explanatory variables was estimated. Then Hausman test is applied to decide between fixed and random effects model and the results were reported in Supplementary Table 2. Chi square statistics of first regression reveals that fixed effect model is appropriate for model estimation. Similarly, for rice yield and maize yield the same test was applied.
District fixed effects
The missing and unobserved factors including inputs like irrigation, fertility of land etc. are not included in the model. Annual yield of wheat, rice and maize are dependent variables, and are used in three alternative regressions against annual precipitation and temperature. Results are reported in Table 1. For absorbing unobserved time invariant determinants of yield variability district fixed effects coefficient is included. The negative value of coefficients of district show lower variability as compared to the positive value of district coefficients.
Table 1 indicates that annual rainfall has negative and significant impact on wheat, rice and maize. These effects are negligible for kharif crops but more impact on Rabi crop such as wheat, it suffers heavily because of high quantity of rainfall in winter season. This implies that more rainfall leads to decrease in the yield productivity of crops in rainy season. Higher temperature affects the yield of wheat, maize and rice positively.
Table 1: Results of panel least square dummy variable method with district fixed effects.
| Climatic Variables | Wheat | Rice | Maize |
| Constant | 3.69916(0.0001)* | 3.803300(0.0005)* | 2.606377(0.0023)* |
| Annual total Rainfall | -0.3650 (0.0001)* | -0.06731(0.0057)* | -0.0460(0.0069)* |
| Annual Total Temperature | 0.18302(0.0023)* | 0.3697(0.0002)* | 2.8301(0.0000)* |
| Trend | 0.01562(0.0000)* | 0.0200(0.0000)* | 0.0164(0.0000)* |
| District Fixed effect | |||
| Hyderabad | 0.1009(0.0000)* | 0.1666(0.0000)* | 0.0850(0.0000)* |
| Badin | -0.3534(0.0000)* | 0.0066(0.7782)* | -0.3743(0.7782) |
| Nawabshah | 0.1835(0.0069)* | 0.354699(0.0075)* | 0.1341(0.0075)** |
| Faisalabad | 0.0624 (0.006)* | -0.107829(0.0001)* | 0.0579(0.0013)** |
| Sialkot | -0.2341(0.0040)** | 0.062662(0.2870) | -0.2291(0.0000)* |
| Jhelum | -0.4454(0.0000)* | -0.090027(0.0530) | -0.4546(0.2271) |
| Bahawalnagar | -0.0720(0.000)* | -0.1352(0.0000)* | -0.0893(0.0033)* |
| Sargodha | -0.0019(0.8935) | 0.0268(0.2936) | 0.0037(0.0000)* |
| Mianwli | -0.3880(0.0000)* | 0.0788(0.4613) | -0.4385(0.0000)* |
| Peshawer | -0.1118(0.0002)* | 0.4159(0.0000)* | -0.0732(0.0000)* |
| Kohat | -0.9941(0.0000)* | 0.0103(0.7677) | -0.9527(0.8058) |
| DI khan | -0.4104(0.0000)* | 0.6729(0.0000)* | -0.4022(0.0000)* |
| Chitral | -0.2933(0.0000)* | 0.4245(0.0000)* | -0.28813(0.039) |
| Lasballa | -0.1447(0.0000)* | -0.1215(0.0000)* | -0.14533(0.0000)* |
| Sibi | -0.2020(0.0000)* | 0.1975(0.0000)* | -0.19660(0.0000)* |
| Bahawalpur | -0.0151(0.0001)* | -0.0396(0.0000)* | -0.03025(0.0000)* |
| Lahore | 0.1057(0.0000)* | 0.04939(0.1629) | 0.107881(0.0000)* |
|
R2 |
0.828210 | 0.701614 | 0.8280 |
| F-stat | 95.1156(0.0000)* | 50.9130(0.0000)* | 112.1492(0.0000)* |
In this table * represent 1 percent level of significance and figures in parentheses are (Prob.) values.
Unobserved district effects, which have been capture by district dummies, have significant impact on annual yield productivity of the crops. Unobserved effects of Hyderabad, Nawab shah, Sargodha and
Lahore have positive and significant impact on crop yield variability. On the other hand, individual effects of Badin, Sialkot, Jhelum, Bahawalnagar, Mianwali, Peshawar, D. I. Khan, Chitral, Lasballa, Sibi and Bahawalpur have negative but significant effect on annual crop yield variability. Base district is Multan which is captured by constant term, also positive and significant. The model has autocorrelation problem; therefore, we use AR process to remove it. In first equation, we use lagged terms until autocorrelation is removed from the model. Durbin Watson statistics in all three models indicate that models do not have autocorrelation problem. This model also has heterogeneity problem, so cross section and time white process is used to rectify it. Moreover, value of R2 is high enough, which indicates the overall goodness of the fit of the given model. First regression shows that 82 percent variation in yield variability of wheat is due to climatic variability. F-statistic is also highly significant, which shows the stability of the model. Similarly, in second and third regressions R2 s are 70.2 and 82.8 percent and F-statistics are highly significant. However, the impact of omitted variables and data inaccuracies may counteract at broad scales (Gong et al., 2003) as suggested by high value of R2.
Table 2: Results of elasticity of crop yield w.r.t climatic variables.
| Variables | Rainfall | Temperature |
| Wheat Yield | -0.469 | 0.138 |
| Rice Yield | -0.091 | 0.293 |
| Maize Yield | -0.059 | 2.138 |
Elasticity of crop yield is also calculated due to percentage changes in mean annual rainfall and temperature. It took the value of coefficient from Table 1, then multiplied it with sample average climate (temperature and precipitation), and divided it by average annual yield. The calculated elasticities are reported in Table 2.
However, one percent increase in rainfall and temperature causes 46.94 percent decrease in annual yield variability of wheat. Elasticities of rice shows that one percent increase in rainfall leads to less than 9 percent decrease in annual yield variability and 5 percent in maize respectively. With temperature, elasticities are smaller. One percent increase in temperature results in 13.8 percent change in wheat yield variability and 29.39 percent in rice Moreover, change in rainfall decreases maize yield variability while temperature has positive impact.
Conclusions and Recommendations
The objective of the study was to quantify the impact of climate change on inter annual yield variability on major crops and offer grounds for sustainable development of agricultural sector both at country and local level. The result shows that rainfall pattern negatively and significantly affects crop yield, while increase in temperature has a positive impact.
So, it is recommended that climate change adaptation strategies should be made by the farmers in order to mitigate their adverse effects which lead to long run increase in crop yield and decrease inter annual yield variability in changing climatic conditions, especially during monsoon season that account for higher amount of rainfall than global averages. It is for the planners to develop such policies that help the farmers to maximize their benefits and reduce cost as a result of climate change. Changing cropping patterns, sowing dates, and crop varieties are some of the measures farmers can take to minimize the risk posed by changing climate.
In interpreting the results, it is important to take into consideration the lack of availability of necessary data. It does not consider the impact of climatic change on crop production through CO2, humidity and solar radiation due to unavailability of wide range of time series data in Pakistan. The study does not take into account detailed study of crop locality due to unavailability of data on land slope, latitude, altitude, and soil type. GIS data is not modified in accordance with the requirements of a typical time series data set. Future work may therefore be necessary to disaggregate climate data into finer temporal scales or similarly disaggregating yield data to finer spatial scales.
Author’s Contribution
Khush Bukhat Zahid: Conducted the study, re-viewed the literature, and wrote the paper. Proposed final recommendations and conclusions
Ghaffar Ali: Edited the write-up and make it pre-cise and comprehensive
Samina Sabir: Provided guidance in analysing data and performed proof reading
Mohammad Fayaz: Performed proof reading of the draft and corrected references.
There is supplementary material associated with this article. Access the material online at: http://dx.doi.org/10.17582/journal.sja/2019/35.1.36.42
References
Chen, C.C. B.A. McCarl and D.E. Schimmelpfennig. 2004. Yield variability as influenced by climate: a statistical investigation. Clim. Change. 66 (1-2): 239-261. https://doi.org/10.1023/B:CLIM.0000043159.33816.e5
Deschenes, O. and M. Greenstone. 2000. The economic impact of climate change evidence from agriculture output and random fluctuations in weather. Department of Economics University of califorrnia. Cost Clim. Change US Agric. 97(1): 354-381.
Dickey, D.A. and W.A. Fuller. 1979. Distribution of the estimators for autoregressive time series with a unit root. J. Am. Stat. Assoc. 74(366a): 427-431. https://doi.org/10.1080/01621459.1979.10482531
ESP. 2016. Government of Pakistan statistical division Islamabad Ministry of Finance.
FRTFCC. 2010. Final Report, Task Force on Climate Change, Planning Commission of Pakistan.
Gong, X. A.G. Barnston and M.N. Ward. 2003. The effect of spatial aggregation on the skill of seasonal precipitation forecasts. J. Clim. 16(18): 3059-3071. https://doi.org/10.1175/1520-0442(2003)016<3059:TEOSAO>2.0.CO;2
GoP. 2016. Pakistan economic survey report. Chapter no. 2, Agriculture, pp. 22-40.
Hanif, U., H. Shabib, R. Syed, K. Ahmad, M. Abdullah and N. Muhammad. 2010. Economic impact of climate change on the agricultural sector of Punjab [with Comments]. Pak. Dev. Rev. 49: 4: 771 -798. https://doi.org/10.30541/v49i4IIpp.771-798
Hausman, J.A. 1978. Specification tests in econometrics. Econometrica. J. Econ. Soc. 1251-1271.
IPCC. 2007. Contribution of working paper group 1 to the fourth assessment report of the inter government panel on climate change. Summ. Policymakers.
IPCC. 2014. Summary for policymakers. In Field, C.B. Barros, V.R. Mastrandrea, M.D. Mach, K.J. Abdrabo, M.K. Adger, N. and V.R. Burkett, V. R. 2014. Climate change: impacts, adaptation, and vulnerability. Part A: global and sectoral aspects. Contrib. Working Group II Fifth Assess. Rep. Intergovernmental Panel Clim. Change, 1-32.
Just, R.E. and R.D. Pope. 1978. SStochastic specification of production functions and economic implications. J. Econ. 7(1): 67-86.
Levin, A. and C.F. Lin. 1993. Unit root tests in panel data: new results. Univ. Calif. San Diego, Econ. Working Paper Series.
Pesaran, M.H. and E. Tosetti. 2011. Large panels with common factors and spatial correlation. J. Econ. 161(2): 182-202. https://doi.org/10.1016/j.jeconom.2010.12.003
SPORE. 2008. Climate change, Spore special issue-August.
White, M.R. 1985. Characterization of information requirements for studies of CO2 effects: Water resources, agriculture, fisheries, forests, and human health. U. S. Dep. Energy.