Optimization of the Cropping Pattern in District Hunza, Gilgit-Baltistan
Optimization of the Cropping Pattern in District Hunza, Gilgit-Baltistan
Fazal Haq*, Asia Parveen, Safdar Hussain and Arshad Hussain
Department of Mathematical Sciences Main Campus, Karakoram International University Gilgi-Baltistan, Gilgit, 15100, Pakistan
Abstract | Agriculture sector having full range of activities has a key role in the economic development of any area. The main problem in agriculture is, making decision for optimum selection of activities. Keeping in view such critical issues; this research study is conducted in District Hunza with the aim to explore the most beneficial cropping pattern for the three major crops wheat, potato and alfalfa grown in the study area and to maximize the net profit per year. The research study deals with statistical facts and figures so quantitative method of research is approached. The growers of the major crops were the targeted population and random sampling technique is used to select the sample. Self made questionnaires, filled through interviewed process from the random selected farmers were used as a tool for collecting primary data. The raw data is tabulated and analyzed using Microsoft Excel. The analyzed data is used to develop the mathematical model. Simplex method is applied to find the optimal solution of the model, which showed 10.18% increase in the net revenue per year.
Received | June 15, 2019; Accepted | February 16, 2020; Published | April 28, 2020
*Correspondence | Fazal Haq, Department of Mathematics, Karakoram International University, Hunza Campus Gilgit-Baltistan, Gilgit, 15700, Pakistan; Email: fazal.haq@kiu.edu.pk
Citation | Haq, F., A. Parveen, S. Hussain and A. Hussain. 2020. Optimization of the cropping pattern in district Hunza, Gilgit-Baltistan. Sarhad Journal of Agriculture, 36(2): 612-616.
DOI | http://dx.doi.org/10.17582/journal.sja/2020/36.2.612.616
Keywords | Linear programming, Simplex method, Optimization, Optimal solution, Cropping pattern
Introduction
Agriculture has a key role in enhancing the economic growth of agricultural countries. The main issue in agriculture sector is making decision for choosing the best among variety of options. Although the farmers grown all types of vegetables and crops using their past experiences, instinct and comparing with neighbors but the lack of knowledge about the most beneficial cropping pattern with efficient resources utilization remained a crucial problem for farmers, so its need to be solved because of the social and economical importance of agricultural commodities due to rapid growth shown in population. Linear programming is a best technique used for solving such issues. For solving such a case Ishtiaq et al. (2004) used LP model to find the optimal crop among wheat, basmati rice, IRRI rice, cotton, sugarcane, maize and potato which are cultivated in Faisalabad division over 2702 thousand acres of irrigated land. The optimal result showed that wheat, cotton and maize were the optimal crops and the net income increased by 2%.
To help the farmers for the selection of profitable crop, Khan et al. (2005) developed LP model to calculate the optimal crop acreage, production and net income of the Bahawalpur division of Punjab. Their result showed that cotton is the most profitable crop among other crops gained total optimal acreage of 10% and the overall optimal usage of land decreased by 1.76%. The net optimal income increased by 3.28% as compared to the farmer decision. Ghulam et al. (2009) used the application of LP to trace out the comparative advantage of strawberry cultivation in subtropical areas of NWFP. The linear programming model suggested 0.68 acres of land should be reserved for strawberry production and 2.8 acres for the production of sugarcane and wheat was not a part of the optimal result. The linear programming model increased the net revenue from Rs.111861 to Rs.161263 with 0.97 acres of unused land. Felix (2013) used linear programming model to help the farmers of Marondera, Zimbabwe to make better decision for the best allocation of scattered resources and to maximize the net income. The findings showed that overall crop acreage decreased by 30% and the net income of farmer’s increased by 35%. For more agricultural productivity, the proper management of resources is most essential. For optimum utilization of resources in multi region Amin et al. (2013) conducted study at three counties of Iran and developed linear programming model for examining the multi-regional cultivation. The result of the study showed that optimum cropping pattern increased the net profit of the regions Babol 6.8%, Babolsar 8.9% and Qaemshahr 5.6%. The multi-regional model will increase the profit of the whole region to 1.4%. The farmer’s income was greatly influenced by the better allocation of land. Aquil et al. (2015) used the agriculture data for five foods crops and developed LP model to find the optimal land allocations for the crops. The LP model was compared to the existing result which showed that the optimal land used was 2752.56 acres as compared to 2409 acres. The maximum profit gained from linear programming model was Rs.1376. Ishtiaq et al. (2005) developed linear programming model to estimate the cropping pattern for the Dera Ghazi Khan District of Punjab. The crops included wheat, cotton, sugarcane; basmati rice and IRRI rice were studied over the 3913 thousand acres of cropped area. The optimal result obtained from linear programming model showed that cotton is the optimal crop reserved 10% of the total land and the net income increased by 2.91% as compared to the farmer’s plan. Sara et al. (2017) used LP model to study the copping pattern in Egypt. They used five-year data from 2008-2012 of 28 crops. The authors come to the consolation that LP results increased the net profit of study area by 6.44%. A fuzzy LP model is developed with the objective of sustainable agriculture and to optimize the profit by finding best cropping pattern (Ziaee et al., 2014). The LP results showed that wheat should be increased to get maximum profit. For more details, the interested readers are referred to Ishtiaq et al. (2004); Felix et al. (2013); Mushtaq et al. (2014); Shreedhar et al. (2015) and Devaroroo et al. (1991).
Objectives
The main objective of current study was to develop a LP model to maximize the net profit gained from three major crops wheat, alfalfa and potato in District Hunza. . The other objectives were;
- • To explore the beneficial cropping pattern for the major crops.
- • To find optimal land allocation for the major crops.
- • Facilitating the farmers for better decision.
- • Familiarizing people to the practical usage of LP for making better decision.
Materials and Methods
Study area
Hunza is situated in the extreme northern part of Pakistan and a district of Gilgit-Baltistan. Hunza has three main geographic subdivisions; lower Hunza, Central Hunza and Upper Hunza. It is situated on 36.26° North latitude and 74.73° East latitude at an altitude of 8200 ft. above sea level and located at a distance of 100 Km from the main city Gilgit. The territory of study area is about 7900 square kilometers. Hunza included in the coldest region of Pakistan, having average temperature 8.9 degree Celsius, where July and August are the warmest months of the year having average temperature 28 degree Celsius. There is only a season of cropping from April to October, so the cultivators grow maximum crops and vegetables possible in the season to fulfill their basic necessities. The major crops grown in the area are wheat, potato and alfalfa.
Data and method of solution
This research study is based on primary data collected through self-made questionnaires and face to face interview process in District Hunza. Two stage sampling techniques are applied for collecting data. In the first stage the farmers of the study area are divided into three groups; the potato growers, the wheat growers and the alfalfa growers and in the second stage randomly 63 farmers (21 farmers from each group) are interviewed for the study and questionnaires are filled on the spot. The optimal solution of formulated LP model is obtained using Simplex method.
LP model formulation
LP is one of the best approaches of mathematical optimization that utilizes numerous connected concepts of mathematics to allocate limited resources among competing demands in an optimal way. It uses models in mathematics to describe problems of concern. The application of LP optimization tool is dependent on following assumptions:
- • Decision variables to be optimized,
- • Objective function that must be maximized in case of profit,
- • Constraints.
Explanation of above components of LP model is as follows;
Decision variables
Variables are the combination of mathematical expressions in the objective function to be optimized by the model. The goal is to find values for the coefficient of decision variables to provide the best rate of the objective function.
Objective function
The Objective Function is a mathematical expression that combines the decision variables and their coefficients to achieve the goal of optimum benefits and is expressed as follows;
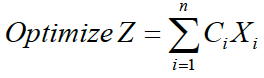
Constraints
The constraints are mathematical expressions to represent limits in the model related to available resources. The model assesses and identifies possible solutions that respect these limits in order to achieve the optimum objective function. Mathematically constraints are expressed as:
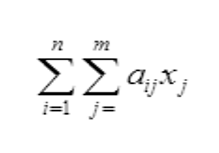
Where aij are the coefficients for the introduced constraints and bi are the limits for the constraints.
The LP Model formulated here is based on data collected from the farmers of study area. The analyzed data is displayed in Table 1.
The farmers of the study area have total 1.101461 acres of land. The farmers used their past experiences and allocate 0.4166 acres of land for the production of wheat, 0.3693 acres of land for the production of alfalfa and 0.315476 acres of land for the production of potato. The objective of study refers to the best allocation of land in acres for the major crops, to maximize the profit and identify beneficial cropping pattern among the major crops. The resources include were land, labor, fertilizer and capital. The decision variables are:
Z= Net returns from all crops; x1=Allocation of land for the growth of wheat in acres; x2=Allocation of land for the growth of potato in acres; x3=Allocation of land for the growth of Alfalfa in acres.
The formulated LP model based on summarized data for this comparative study is given by:
Maximize Z =30,706 x1 + 32,310 x2 + 24,000 x3
Subject to constraints:
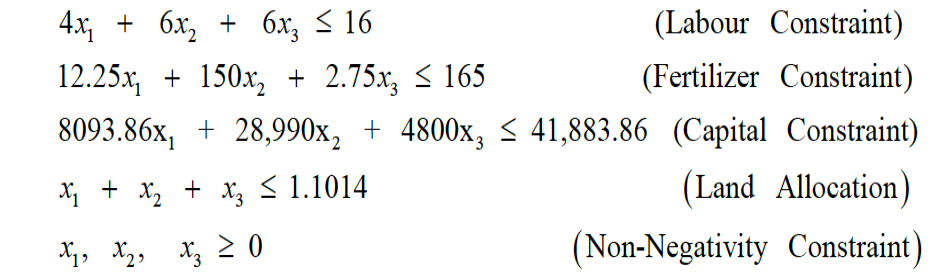
Table 1: Linear programming matrix.
| Activities | Wheat | Potato | Alfalfa | ||
| Objective function | 30,706 | 32,310 | 24,000 | Maximize available | |
| Resources | Units | ||||
| Labor | Person days | 4 | 6 | 6 | ≤ 16 |
| Fertilizer | Kg | 12.25 | 150 | 2.75 | ≤ 165 |
| Capital | Rupees | 8093.86 | 28990 | 4800 | ≤ 41883.86 |
| Land | Acres | 1 | 1 | 1 | ≤ 1.1014 |
Results and Discussion
Linear programming model is developed and solved by simplex method, which gave an optimum result. The optimal result obtained for land allocation from the LP model is compared with the farmer’s decision is presented in Table 2. The allocation of land for the major crops in a best way is obtained from the LP model which shows that the crop acreage of potato increased by 248 % and wheat decreased by 99.634% as compared to the farmers plan, where alfalfa crop is not a part of the optimal result. The comparative result showed that the farmers had reserved more land for alfalfa production but the result obtained was not satisfactory as compared to the LP model, which suggest to crop potato to large extent to get maximum profit and advantage from the well utilized resources.
Table 2: Comparison of land allocation under LP solution with farmer’s plan.
| Crops | Farmers plan (Acres) | Optimal solution (Acres) plan | Percentage of farmers |
| Wheat | 0.4166 | 0.0015244 | 0.366 |
| Potato | 0.315476 | 1.099875 | 348.63 |
| Alfalfa | 0.369318 | 0 | 0 |
| Total | 1.101394 | 1.1013994 | 100 |
The comparison result of land allocation was graphed in Figure 1, the graph gives better understanding of the differences between the results.
As the farmers used the available resources on the basis of their past experiences but the LP model best utilized the resources and maximizes the profit. For more clarity the resources utilization for the major crops under LP model is compared with the farmer’s decision in Table 3.
The results obtained from the Table 2 and Table 3 gives the clear picture of the comparison of LP results and formers plane. From these tables we conclude that if the famers of the study area by allocating land and utilizing the given resources according to LP results the net profit maximizes up to Rs. 35,583.786 per year. This shows an improvement of 10.18% as compared to the farmer’s traditional method. The results are tabulated below.
The overall picture of the optimal results shows that farmers should use linear programming model for decision making in order to get more profit. The final profit was compared and the result is shown in Figure 2.
Table 3: Comparison of resource utilization.
|
Farmers Plan(Acres) |
||||||
| Resource | Land (Acres) | Fertilizer (Kg) |
Labor ( Days) |
Capital (Rs.) | ||
|
Available Usage % of Usage Unused % of Unused |
1.1014 | 165 | 16 | 41883.86 | ||
| 1.1014 | 53.440 | 5.775 | 14,290.277 | |||
| 100 | 32.39 | 36.09 | 34.12 | |||
| 0 | 111.56 | 10.225 | 27,593.58 | |||
| 0 | 67.61 | 63.91 | 65.88 | |||
|
Linear Programming Model |
||||||
|
Available Usage % of Usage Unused % of Unused |
1.1014 | 165 | 16 | 41883.86 | ||
| 1.1014 | 165 | 6.6 | 31897.73 | |||
| 100 | 100 | 41.25 | 76.16 | |||
| 0 | 0 | 9.4 | 9986.1307 | |||
| 0 | 0 | 58.75 | 23.84 | |||
Table 4: Comparison of net profit from potato.
| Farmers plan in Rs. | Optimal solution in Rs | Percentage of farmers Plan |
| 32,296.21 | 35,583.786 | 110.179 |
Conclusions and Recommendations
For this study LP model is developed to maximize the profit of major crops of district Hunza. The LP model best allocates the land and maximizes the profit. The comparison of obtained results from LP model to the farmer’s traditional plan showed an improvement of 10.18%. The result depicts that LP is a superior and suitable model for use in any decision making situation because of its highly appreciated results. So it is strongly recommended for putting the suggestions of linear programming model into practice in their daily life to get maximum advantage from available resource with lowest expenses.
The following suggestions are made on the bases of findings of the research for the betterment of the agriculture sector in the study area.
- • For enhancing income of the people potato should be produced at large extent because it is beneficial crop.
- • To get maximum profit LP results suggest that alfalfa should not grow in the study area.
- • Best quality of seed and suitable fertilizer at proper ratio should be used by the farmers for more production
- • Awareness sessions for the farmers regarding scientific methods should be conducted by the government (Agriculture department).
- • Market infrastructure and adequate rate of fertilizer should be provided to the famers by government to encourage farmers for the production of potato.
Novelty Statement
This research paper has focused on maximizing the profit obtained from major crops cultivated in district Hunza, Gilgit-Baltistan by best allocation of available resources. Adoption of mathematical approach into practice in daily life of farmers helps to best utilization of available resources and get optimum profit.
Author’s Contribution
FH supervised the overall activities. AP compiled and interpreted the results. SH compiled and interpreted the results. AH helped in data analysis and model solution.
Conflict of interest
The authors declare no conflict of interest.
References
Amin, A., F.S. Bidabadi, R. Joolaei and A. Keramatzadeh. 2013. Managing cropping patterns agricultural crops of three counties of Mazandarn province of Iran. Int. J. Agric. Crop Sci. 5(6): 596-602.
Aquil, A., N.A. Sofi, M. Ahmad and B.A. Bhat. 2015. Decision making in agriculture: A linear programming approach. Int. J. Modern Math. Sci. 12(2): 160-169.
Devaroroo, M.D., D.M. Kondap and A.R. Suryavanshi. 1991. A linear programming model for optimal cropping pattern for the pus project Maharashtra India. J. Maharashtra Agric. Univ. 16(1): 4-7.
Felix., M., 2013. Optimum combination of crop farm enterprises: A case study of a small-scale farm in marondera, Zimbabwe. Int. Res. J. 2(1): 60-65.
Felix., M., Judith, M. Jonathan and S. Munashe. 2013. Modeling a small farm livelihood system using linear programming in bindura, Zimbabwe. Res. J. Manage. Sci. 2(5): 20-23.
Ghulam, S.A., M. Ishaq and S. Ahmad. 2009. Cost and revenue analysis of strawberry production in the sub-tropical areas of NWFP, Pakistan. Pak. J. Life Soc. Sci. 7(1): 59-65.
Ishtiaq, H., M.A. Raza, I.A. Khan and R. Ilahi. 2005. Use of linear programming model to determine the optimum cropping pattern, production and income level: A case study from dera ghazi khan division. J. Agric. Soc. Sci. 1(1): 32-34.
Ishtiaq, H., M.A. Raza, M. Khalil and R. Ilahi.2004. Determination of optimum cropping pattern in the Faisalabad Division Pakistan. Int. J. Agric. Bio. 6(5): 901-903.
Khan, I.A., M.A. Khan , I. Hassan, N. Cheema and R. Maryam. 2005. Use of Linear Programming Model to Determine Optimum Cropping Pattern in Bahawalpur, Punjab, Pakistan. Pak. J. Life Soc. Sci. 3(1-2): 21-23.
Mushtaq, L., S.A. Mir, S. Maqbool and I. Khan. 2014. Modeling crop pattern system using linear programming. Golden Res. Thoughts. 3(12): 1-4.
Sara, O., M. Elkholy and R.M. Kansoh. 2017. Optimization of the cropping pattern in Egypt. Alexandria Eng. J. 56(4): 557–566. https://doi.org/10.1016/j.aej.2017.04.015
Ziaee, S., K. Hadis, K. Elham and S. Samira. 2014. The Determination of Optimal Cropping Pattern Using Mathematical Programming with an Emphasis on Sustainable Agriculture. J. App. Environ. Biol. Sci. 4(5): 21-25.








