Nonlinear Growth Functions for Body Weight of Thalli Sheep using Bayesian Inference

Farhat Iqbal1, Abdul Waheed2,*, Zil-e-Huma3 and Asim Faraz2

1Department of Statistics, University of Balochistan, Quetta

2Faculty of Veterinary Sciences, Bahauddin Zakariya University, Multan

3Department of Zoology, Sardar Bahadur Khan Women’s University, Quetta

ABSTRACT

This article deals with the Bayesian approach for estimating the parameters of nonlinear growth functions used for modelling the body weight of farm animals. Gompertz, Brody, Von Bertalanffy and Logistic growth models were employed on the basis of nonlinear least squares and Bayesian methods. Using the monthly body weight data of 2070 weight records of Thalli sheep from birth to 24 months of age for both sexes (male and female) and type of births(single and twin), the estimates of parameters and their credible intervals were obtained from posterior distributions. The overall goodness of fit of classical method was calculated; namely, Akaike information criterion (AIC), Bayesian information criterion (BIC), coefficient of determination (R2) and root mean square error (RMSE). Deviance information criterion (DIC) and the square of correlation (R2) between observed body weight and the predicted value’s marginal density means and RMSE were used as evaluation measures in the Bayesian setup. Both approaches were strongly in favor of the Brody model as the best fit model than the competing nonlinear growth models for Thalli sheep. Results displayed that complex nonlinear functions can be easily fitted to weight-age data of animal via Bayesian approach.

Article Information

Received 08 October 2018

Revised 09 November 2018

Accepted 14 November 2018

Available online 10 May 2019

Authors’ Contribution

AW designed the research, conducted the experiments and collected the data. FI analyzed the data, interpreted the results and wrote the manuscript. ZH and AF interpreted the results and revised the manuscript.

Key words

Bayesian, Body weight, Nonlinear growth models, Model fitting.

DOI: http://dx.doi.org/10.17582/journal.pjz/2019.51.4.1421.1428

* Corresponding author: dobaara@gmail.com

0030-9923/2019/0004-1421 $ 9.00/0

Copyright 2019 Zoological Society of Pakistan

Introduction

Increase in body weight of animal with respect to time is commonly referred as growth and is one of the most important characteristics when determining animal performance. Several nonlinear functions have been adopted to ascertain the sigmoidal relationship between body growth of animal and age. Researchers may be interested in fitting such functions to describe the growth trend of an animal. These, among others, include the Gompertz (Laird, 1965), Brody (Brody, 1945), Von Bertalanffy (Bertalanffy, 1957) and Logistic (Nelder, 1961) nonlinear functions. The parameters of these nonlinear growth models considered as selection criteria for breeding purposes present some interesting biological interpretations. Therefore, it is important to carefully consider the best non-linear model describing a particular growth pattern in order to describe the studied breed standards and to determine managerial problems in a flock, and especially, the best slaughtering time.

There is a growing interest in modeling the growth of sheep. The previous researchers have successfully used nonlinear growth functions to capture the relationship between the body weight and time in different breeds of small ruminants (Tekel et al., 2005; Karakus et al., 2008; Keskin et al., 2009; Kum et al., 2010; Tariq et al., 2013; Kopuzlu et al., 2014; Hojjati and Hossein-Zadeh, 2017). It has been reported that the shape of nonlinear growth curves can vary based on the species of animal, the trait and the environment (Akbas et al., 1999; Topal et al., 2004).

Sheep is a small ruminant known as one of the major livestock resources of Pakistan. Thalli is a medium sized mutton type sheep breed of Thalli desert of the Punjab province of Pakistan reared primary for meat production. Thalli have thin tails and white body with brown and black head and black spotted lower legs. Waheed et al. (2016) comparatively examined some nonlinear growth functions for estimating growth curve parameters in Thalli sheep breed.

The nonlinear regression is popular method of estimation among practitioners for fitting various growth curves. This classical or frequentist method treats the parameters of growth model as constants and estimates the unknown parameters using iterative algorithms. The Bayesian approach, as an alternative, treats the parameters of the model as random variables and inference on parameters is made using their posterior distributions without the assumption of normality of the data. The Bayesian approach incorporates the parameters’ uncertainty and produces accurate estimates along with the credible intervals, in some cases. Efficient Markov Chain Monte Carlo (MCMC) methods have made the Bayesian method a popular choice among researchers from various disciplines as an alternative to the frequentist approach.

Although nonlinear least squares method is a popular choice for fitting growth models, the choice of starting values of parameters and the non-convergence of algorithm are common issues faced by researchers. This study shows how the Bayesian approach, on the other hand, can be easily adopted to avoid the issues of nonlinear least squares. The results of both methods can be compared based on goodness of fit statistics. To the best of our knowledge, no previous studies have been conducted to fit nonlinear growth curves to Thalli sheep using the Bayesian approach. The aim of the present study was to comparatively examine some nonlinear growth models i.e. Gompertz, Brody, Von Bertalanffy and Logistic for modeling the weight-age relationship in Thalli sheep on the basis of Bayesian inference and to ascertain the best fitted model to the data.

 

Materials and methods

Data

In the present study, the data from birth to two years of age on weight in kilogram (kg) of 207 Thalli sheep breed were used. The data were collected from Livestock Experiment station Rakh Gulaman, Bhakkar (31° 37ʹ 60ʹʹ N and 71°03ʹ 60ʹʹ E at 171 m altitude), Pakistan. The weight-age data consist of 95 males and 112 females; 185 single and 22 twin birth sheep. The sheep records were measured at birth weight, 1st, 2nd, 3rd, 4th, 6th, 9th, 12th, 18th, and 24th months of age. The animals were weighed with sensitivity scale of 50 g. The weight-age relationship for Thalli sheep was described on the basis of individual body weights of these sheep.

Statistical analysis

In the present study, four popular nonlinear growth models were used. Consider the model:

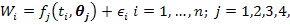
Where, Wi is the recorded body weight of ith animal, n is the total number of animals, ti is the time at which ith observation was recorded, ϵi~N(0, σ2) is the error term. The function fj (.) represents one of the four nonlinear growth curve function with j=1,2,3,4 for the Gompertz, Brody, Von Bertalanffy and Logistic functions, respectively. The unknown parameter vector for these growth curves is θj where θj = (θ1,θ2,θ3). The exact mathematical form of the nonlinear models used to model the weight-age relationship of Thalli sheep are as follows:

Gompertz Model

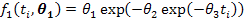
Brody Model

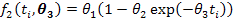
Von Bertalanffy Model

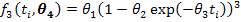
Logistic Model

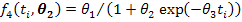
In all these nonlinear models, ti represents the time (in days), the first parameter θ1 is the measure of the mature weight of the adult animal as age approaches infinity (also known as the asymptotic weight). Note that θ1 is not the maximum weight an animal can attain. The second parameter θ2 is the constant related to the birth weight of the animal and the third parameter θ3 is a function of the ratio of maximum growth rate to mature weight commonly known as the maturity index.

First, the classical nonlinear least squares (NLS) approach was adopted to estimate the unknown parameters of various growth models. These growth models were fitted to individual animal to account for possible bias that may arise in the growth parameters due to consecutive and repeated measurements. The averages of the estimated parameter values and evaluation measures were then used for further analysis. The Gauss-Newton algorithm in nls2 function of R program (R Development Core Team, 2014) was utilized for the estimation of unknown parameters. The fit from each growth model was evaluated using various evaluation measures such as Akaike information criterion (AIC), Bayesian information criterion (BIC), the correlation coefficient between the fitted and actual body weights (Corr), the coefficient of determination (R2) and the root mean square error (RMSE). Smaller values of AIC, BIC, are desired whereas values of Corr and R2 close to 1 indicate a better fit.

The joint posterior distribution for the unknown parameters of each growth model separately for male, female, single and twin sheep were obtained through the Bayesian inference. The best model, for both sexes (male and female) and type of births (single and twin), is selected based on the lowest Deviance information criteria (DIC) and highest R2 values. The DIC compares the overall predictive ability for model assessment. The model with the smallest value of DIC is preferred. However, small DIC difference in competing models needs further investigation (Spiegelhalter et al., 2002). Therefore, the following rule was used to check the significant difference in the values of DIC; the difference is considered not significant if its value is less than 3 whereas a difference of 3 and more is considered significant (Spiegelhalter et al., 2002). In addition, the square of the correlation between observed body weight and the predicted value’s marginal densities means (R2) was also calculated. Similarly, R2 values close to unity indicate accurate fit to the observed weight.

The Bayesian statistical analysis was also conducted using the R program. The JAGS program (Plummer, 2003) was used to obtain the posterior samples of the parameters of models through R2 jags package of Su and Yajima (2015). For both unknown parameter vector and for the precision parameter, non-informative prior distributions were used. More specifically, for each parameter a normal distribution with mean 0 and standard deviation 100 i.e., θi~N(0,1002) and for the precision parameter a gamma distribution i.e., Ga(0.001,0.001) were considered. A total of 30,000 MCMC samples were generated discarding initial 10,000 as a burn-in sample. A thinning of every 5th sample produces a sample of 4000 for the posterior analysis. The convergence of MCMC chain was verified using the CODA program (Best et al., 1995) and Geweke convergence criteria (Geweke, 1992). These diagnoses confirmed the good mixing performance and fast convergence of MCMC chains. The R codes used in this study can be provided upon request.

 

Table I.- Comparison of various growth curves through frequentist approach.

Model	AIC	BIC	Corr.	R2	RMSE	Model	AIC	BIC	Corr.	R2	RMSE
Male						Single
Gompertz	47.4	48.6	0.9921	0.9840	1.782	Gompertz	45.8	47.0	0.9912	0.9824	1.640
Brody	34.8	36.0	0.9974	0.9948	0.985	Brody	34.5	35.7	0.9965	0.9931	0.963
Von Bertalanffy	43.8	45.0	0.9941	0.9882	1.510	Von Bertalanffy	42.6	43.8	0.9933	0.9865	1.411
Logistic	53.7	54.9	0.9859	0.9712	2.416	Logistic	51.6	52.9	0.9852	0.9699	2.182
Female						Twin
Gompertz	44.2	45.4	0.9904	0.9783	1.568	Gompertz	44.7	46.0	0.9904	0.9807	1.578
Brody	34.3	35.5	0.9957	0.9914	0.948	Brody	34.7	35.9	0.9959	0.9918	0.982
Von Bertalanffy	41.4	42.6	0.9924	0.9848	1.320	Von Bertalanffy	41.9	43.1	0.9924	0.9849	1.380
Logistic	49.6	50.8	0.9844	0.9685	1.958	Logistic	50.1	51.3	0.9843	0.9681	2.050

AIC, Akaike information criteria; BIC, Bayesian information criteria; SD ratio, standard deviation ratio; Corr., correlation coefficient between actual and predicted body weight; R2, coefficient of determination; RMSE, root mean square error. Lowest AIC values in bold represent the best model.

 

Table II.- Comparison of various growth curves for body weight through Bayesian approach.

Model	DIC	Comparison	Difference	R2	RMSE
Male
Gompertz	52.2	Gompertz – Brody	13.8*	0.9828	1.836
Brody	38.4	–	–	0.9944	1.014
Von Bertalanffy	47.8	Von Bertalanffy – Brody	9.4*	0.9877	1.541
Logistic	57.7	Logistic – Brody	19.3*	0.9662	2.620
Female
Gompertz	49.1	Gompertz – Brody	11.2*	0.9783	1.568
Brody	37.9	–	–	0.9909	0.966
Von Bertalanffy	46.7	Von Bertalanffy – Brody	8.8*	0.9762	1.414
Logistic	53.9	Logistic – Brody	16.0*	0.9646	2.059
Single
Gompertz	50.7	Gompertz – Brody	12.5*	0.9804	2.035
Brody	38.2	–	–	0.9860	1.075
Von Bertalanffy	47.2	Von Bertalanffy – Brody	9.0*	0.9841	1.463
Logistic	55.8	Logistic – Brody	17.6*	0.9653	2.337
Twin
Gompertz	49.6	Gompertz – Brody	11.1*	0.9788	1.639
Brody	38.5	–	–	0.9909	1.031
Von Bertalanffy	46.6	Von Bertalanffy – Brody	8.1*	0.9840	1.419
Logistic	53.9	Logistic – Brody	15.4*	0.9649	2.147

DIC, deviance information criteria; R2, coefficient of determination. Lowest values of DIC are in bold. * Significant.

 

Results and discussion

The average values of evaluation measures obtained from fitting nonlinear growth models through NLS are given in Table I. High R2 values for all growth models indicated a significant relationship between age and weight of animal. For both sexes and types of births, the Brody model provided the best fit. For instance, for male Thalli sheep, the AIC/BIC values for the Brody (34.8/36.0) were observed as the lowest followed by Von Bertalanffy (43.8/45.0), Gompertz (47.4/48.6) and Logistic (53.7/54.9). The RMSE estimates of Brody growth functions were also the least (0.948–0.985) in all cases. The Corr (0.9974) and R2 (0.9948) values for the Brody model were also highest among the competing models. Similar results were reported for female, single and twin sheep data where the Brody model outperformed other models. The overall assessment of the growth models seems to indicate the best fit of the Brody model for the body weight data of Thalli sheep.

Table II shows the average values of goodness of fit statistics for each growth curve when fitted via Bayesian approach to the weight of Thalli sheep. The difference in DIC values, of the best fit model (having the lowest DIC), with other models are also reported. The lowest DIC values were obtained for the Brody model for all four cases (male, female, single and twin birth data). Large differences between the DIC values of Brody with other models indicated significant difference between the models fit. In other words, the Brody model provided significantly better fit than other competing growth models. R2 values (0.9860 to 0.9944) obtained for the Brody model were also found higher than R2 values other models. The Von Bertalanffy, Gompertz and Logistic models followed the Brody model in terms of better fit. These results also confirmed that among four nonlinear growth models, the Brody model provided the best fit. Hence, both NLS and Bayesian approach selected the same (Brody) model as the best growth model for Thalli sheep. The Logistic model does not seem appropriate for describing the weight-age relationship of Thalli sheep.

The posterior summary statistics of parameters of all growth curves for male / female and single / twin sheep are summarized in Tables III and IV, respectively. The estimates of median, mean along with their standard deviations (SD) and 95% Bayesian confidence intervals (also known as credible intervals) for each parameter are reported. The posterior distributions of parameters are used to obtain these estimates. The SDs of the posterior distribution are similar to the approximate estimates of the standard error of the parameters. In all cases, the estimates of parameters are within the 95% Bayesian confidence intervals. This reflects the advantage of the Bayesian approach for modelling the complex nonlinear functions, particularly is small data sets where the classical method often fails to converge.

The parameter θ1, in all four nonlinear growth functions, is an estimate of the mature weight of the adult animal. From Table III, the highest estimated mature weight was observed for the Brody model for both male (52.82kg) and female (40.93kg) sheep whereas the lowest estimated mature weight was obtained for the Logistic model for male (44.51kg) and female (36.52kg). The difference between the largest and smallest mature weight was about 8.0kg for male and 7.0 kg for female sheep. Not many variations were observed for the Gompertz and Von Bertalanffy equations as the estimates for mature weight were almost similar. The mature live weights of male Thalli sheep were found higher than that of female sheep in all models.

 

Table III.- Posterior summary statistics of parameters of the growth curves for male / female data.

Model		Median	Mean	SD	95% credible ıntervals
					2.5%	97.5%
Gompertz	β1	47.390 / 37.611	47.616 / 37.764	3.220 / 2.527	42.086 / 33.440	54.513 / 42.963
	β2	2.027 / 1.912	2.062 / 1.954	0.250 / 0.264	1.704 / 1.588	2.654 / 2.602
	β3	0.007 / 0.007	0.007 / 0.007	0.001 / 0.002	0.005 / 0.005	0.010 / 0.011
Brody	β1	52.504 / 40.474	52.820 / 40.929	2.967 / 2.167	48.007 / 37.265	59.634 / 45.665
	β2	0.925 / 0.905	0.925 / 0.906	0.018 / 0.024	0.891 / 0.861	0.963 / 0.956
	β3	0.003 / 0.004	0.003 / 0.004	0.000 / 0.003	0.003 / 0.003	0.004 / 0.005
Von Bertalanffy	β1	48.247 / 38.211	48.292 / 38.343	2.462 / 2.238	43.498 / 34.286	53.324 / 43.165
	β2	0.512 / 0.491	0.516 / 0.499	0.039 / 0.052	0.456 / 0.429	0.600 / 0.619
	β3	0.006 / 0.007	0.006 / 0.007	0.001 / 0.003	0.004 / 0.004	0.008 / 0.014
Logistic	β1	44.733 / 36.433	44.506 / 36.524	2.559 / 2.527	39.038 / 31.589	48.606 / 41.768
	β2	5.257 / 4.680	5.501 / 4.947	1.365 / 1.296	3.433 / 3.112	8.893 / 8.383
	β3	0.011 / 0.011	0.011 / 0.010	0.002 / 0.076	0.008 / 0.007	0.018 / 0.018

SD, standard deviation.

 

Table IV.- Posterior summary statistics of parameters of the growth curves for single / twin birth data.

Model		Median	Mean	SD	95% credible ıntervals
					2.5%	97.5%
Gompertz	β1	42.512 / 38.625	42.697 / 38.880	2.946 / 3.313	37.824 / 33.292	48.505 / 46.023
	β2	1.960 / 2.014	1.998 / 2.156	0.256 / 0.625	1.639 / 1.671	2.623 / 4.049
	β3	0.007 / 0.006	0.007 / 0.007	0.002 / 0.002	0.005 / 0.004	0.011 / 0.013
Brody	β1	46.492 / 43.115	46.706 / 43.513	2.472 / 3.423	42.583 / 38.434	52.137 / 50.813
	β2	0.913 / 0.921	0.914 / 0.922	0.022 / 0.023	0.874 / 0.879	0.958 / 0.969
	β3	0.004 / 0.003	0.004 / 0.003	0.001 / 0.001	0.003 / 0.002	0.005 / 0.004
Von Bertalanffy	β1	43.245 / 39.425	43.321 / 39.566	2.317 / 2.581	38.911 / 34.867	48.171 / 45.046
	β2	0.499 / 0.508	0.505 / 0.515	0.044 / 0.048	0.441 / 0.448	0.607 / 0.623
	β3	0.006 / 0.005	0.006 / 0.006	0.001 / 0.001	0.004 / 0.004	0.009 / 0.008
Logistic	β1	40.637 / 36.997	40.567 / 36.988	2.468 / 2.562	35.487 / 31.880	45.262 / 41.981
	β2	4.927 / 5.122	5.181 / 5.365	1.318 / 1.319	3.262 / 3.400	8.572 / 8.671
	β3	0.011 / 0.010	0.011 / 0.010	0.003 / 0.003	0.007 / 0.007	0.018 / 0.017

SD, standard deviation.

 

From Table IV, the highest estimated mature weights, 46.71 kg for single sheep and 43.51 kg for twin sheep, were obtained by the Brody model. The lowest mature weight for single (40.57 kg) and twin (36.99 kg) sheep were obtained from the Gompertz model. The difference between the largest and smallest mature weight was about 6.0 kg for both single and twin sheep. The difference between the estimates of mature weights of both types of birth was found smaller. This may indicate that birth types may not affect the asymptotic weight of animals in Thalli sheep. Higher estimates of θ1 may indicate heavy adult Thalli sheep and may also indicate that these sheep require more time to reach maturity, in other words slow growth of animals. As indicated by Costa et al. (2007), the Brody model with highest values of θ1 overestimates the mature weight.

The parameter θ2, known as the integrated constant, is related to the proportion of growth after birth and has no biological interpretation. The highest estimates of these parameters for male (5.50 kg) and female (4.94 kg) were obtained from the Logistic model (Table III). Note that the Logistic model had the lowest mature weights. This indicates a negative correlation between parameters θ1 and θ2. For the Brody model, the estimates of θ2 for male and female sheep were 0.93 kg and 0.91 kg, respectively. The smaller values of θ2 for the Brody model is also an indication of negative correlation with the larger values of parameter θ1. Similar findings were observed for single and twin sheep from Table IV.

The parameter θ3 provides the estimate of the growth speed and also known as the maturity rate of animal. High maturity rate is an indication of animal maturing early and vice versa. The highest maturity rate for all cases (approximately 0.011 kg) obtained from the Logistic model indicate a lower time to reach maximum growth. The Brody model with the lowest maturity rate (approximately 0.004 kg) indicates animals reach maturity late in life. Negative correlations between the parameter θ1 (mature weight) and parameter θ3 (maturity rate) of animals in all four cases were observed. These findings show that fast growing Thalli sheep do not gain a large mature weight as compared to those sheep that mature slowly in earlier life.

Parameters of all growth models were found significant (Tables III, IV). Next, we compare the estimated weights of each nonlinear model. Table V shows the observed and estimated average weights of both male and female sheep from birth to two years of age. The estimated average weights obtained from the Brody model, for both sexes, were found very close to the observed body weights of animals. The Brody model also provided accurate estimates of body weights for single and twin sheep from birth to two years of age of Thalli sheep (Table VI). These results further confirm the better fit of the Brody model for growth of Thalli sheep.

Figure 1 shows the Bayesian Brody growth curve fitted to both sexes and type of births along with 95% credible intervals. The curves in all cases were found accurate in predicting the actual body weights of Thalli sheep. These figures are in line with the results of Table I where the evaluation measures of the Brody model were found better than other competing models. Moreover, differences in the growth curves of both sexes were observed but not in type of births. Higher weights of male Thalli sheep may be due to hormonal and physiological differences than female sheep. Gbangboche et al. (2008) reported similar findings for Dwarf sheep, Daskiran et al. (2010) for Norduz sheep and Hojjati and Hossein-Zadeh (2017) for Mehraban sheep.

 

Table V.- Observed and estimated average weights of male / female sheep from various growth curves for one to 720 days of age through Bayesian approach.

Age (days)	Observed weight (kg)	Estimated weight (kg)
		Gompertz	Brody	Von Bertalanffy	Logistic
1	3.68 / 3.48	6.13 / 5.43	4.09 / 3.96	5.57 / 4.98	6.92 / 6.22
30	8.42 / 7.65	8.84 / 7.83	8.63 / 7.79	8.68 / 7.90	9.02 / 8.04
60	12.66 / 11.32	12.05 / 10.62	12.87 / 11.33	12.21 / 10.90	11.67 / 10.31
90	16.81 / 14.95	15.52 / 13.58	16.69 / 14.49	15.84 / 13.93	14.79 / 12.92
120	21.06 / 18.07	19.05 / 16.54	20.13 / 17.30	19.40 / 16.85	18.25 / 15.79
180	26.61 / 21.81	25.78 / 21.81	26.02 / 22.04	25.91 / 22.08	25.57 / 21.67
270	31.47 / 25.90	33.91 / 28.34	32.88 / 27.41	33.59 / 28.04	34.76 / 28.89
360	37.36 / 31.31	39.39 / 32.38	37.93 / 31.23	38.88 / 31.99	40.14 / 33.09
540	43.48 / 35.12	44.80 / 36.11	44.42 / 35.90	44.56 / 36.00	43.76 / 35.94
720	48.54 / 38.78	46.67 / 37.26	48.02 / 38.30	46.82 / 37.49	44.38 / 36.43

Estimated weights close to observed weights are in bold.

 

Researchers have applied various growth models for modeling the growth of different species of animal. Each model has a unique mathematical form and models the growth of animal based on the characteristics such as genotype and environmental variation in data. In this study the Brody, Von Bertalanffy and Gompertz functions were all found adequate to predict the body weight of Thalli sheep. The Brody model was found more accurate in predicting the birth weight of Thalli sheep and has better overall fit.

 

Table VI.- Observed and estimated average weights of single / twin birth sheep from various growth curves for one to 720 days of age through Bayesian approach.

Age (days)	Observed weight (kg)	Estimated weight (kg)
		Gompertz	Brody	Von Bertalanffy	Logistic
1	3.64 / 3.01	5.84 / 5.01	4.09 / 3.45	5.33 / 4.55	6.62 / 5.84
30	8.15 / 6.80	8.43 / 7.15	8.38 / 7.01	8.31 / 7.01	8.61 / 7.47
60	12.15 / 10.13	11.47 / 9.67	12.34 / 10.36	11.65 / 9.79	11.11 / 9.49
90	16.05 / 13.72	14.72 / 12.40	15.88 / 13.39	15.04 / 12.66	14.01 / 11.84
120	19.74 / 16.94	17.99 / 15.19	19.03 / 16.13	18.33 / 15.48	17.22 / 14.46
180	24.38 / 20.95	24.14 / 20.56	24.38 / 20.86	24.25 / 20.69	23.87 / 20.06
270	28.88 / 24.93	31.36 / 27.16	30.47 / 26.43	31.07 / 26.94	32.07 / 27.56
360	34.53 / 30.39	36.07 / 31.70	34.86 / 30.59	35.65 / 31.33	36.79 / 32.41
540	39.45 / 34.80	40.56 / 36.34	40.33 / 36.05	40.41 / 36.17	39.93 / 36.09
720	43.70 / 39.54	42.01 / 37.99	43.24 / 39.15	42.22 / 38.18	40.46 / 36.83

Estimated weights close to observed weights are in bold.

 

A detailed comparison on the findings of the current study with other similar studies may seems difficult as literature on modeling weight-age relationship of sheep data through the Bayesian approach is not available. However, the frequentist approach has been extensively used in the past and the Brody model has been found as the best nonlinear model in many studies (Akbas et al., 1999; Bilgin et al., 2004; Gbangboche et al., 2008; Kopuzlu et al., 2014; Hojjati and Hossein-Zadeh, 2017). On the contrary, the Gompertz (Lewis et al., 2002; Topal et al., 2004; Waheed et al., 2016), Von Bertalanffy (Topal et al., 2004), Richards (Goliomytis et al., 2006; Hossein-Zadeh, 2015), and Morgan-Mercer-Flodin (Tariq et al., 2013) have been found appropriate for modeling growth in various sheep. The Brody and Gompertz models were found to efficiently explain the growth in Beetal goat (Waheed et al., 2011). The results of Sieklicki et al. (2016) concluded that Brody model the growth rate of Texel male lamb better than the Gompertz, Logistic and Von Bertalanffy models. Balan et al. (2017) also found the Brody model as the best model for Mecheri breed of sheep of India. We emphasize again that all previous studies on body growth modeling of sheep employed the frequentist approach. The approach used in this research is novel and different as it provides the Bayesian inference for modeling the growth of sheep data.

 

Conclusion

This study adopted the Bayesian approach for modeling the body weight-age relationship of both sexes and type of births from birth to two years of age in Thalli sheep using widely used nonlinear growth models such as the Gompertz, Brody, Von Bertalanffy and Logistic. The estimates of median, mean, standard deviation and credible intervals were obtained from the posterior distributions of the parameter using non-informative priors. The results of the study showed that the Brody model provided the best fit in terms of lower DIC. The Bayesian approach is more suited for complex nonlinear functions. It also incorporates the uncertainty in the parameter. This research may help researchers to select other complex nonlinear growth models for modeling the weight-age relationship that not only best fit the data but adequately describe the body growth of animals.

 

Statement of conflict of interest

The authors declare no conflict of interest.

 

References

Akbas, Y., Taskin, T. and Demiroren, E., 1999. Comparison of several models to fit the growth curves of Kivircik and Daglic male lambs. Turk. J. Vet. Anim. Sci., 23: 537-544.

Balan, C., Kathiravan, G., Thirunavukkarasu, M. and Jeichitra, M., 2017. Non-linear growth modelling in Mecheri breed of sheep. J. Ent. Zool. Stud., 5: 2005-2008.

Bertalanffy, L.V., 1957. Quantitative laws in metabolism and growth. Q. Rev. Biol., 2: 217-230. https://doi.org/10.1086/401873

Best, N.G., Cowles, M.K. and Vines, S.K., 1995. CODA: Convergence diagnostics and output analysis software for Gibbs sampler output, Version 0.3. MRC Biostatistics Unit, Cambridge.

Bilgin, O.C., Esenbuga, N., Macit, M. and Karaoglu, M., 2004. Growth curve characteristics in Awassi and Morkaraman sheep, Part I: comparison of nonlinear functions. Wool Tech. Sheep Breed., 52: 1-7.

Brody, S., 1945. Bioenergetics and growth. Reinhold, New York, USA.

Costa, R.L.D., Afonso, V.A.C. and Quirino, C.R., 2007. Utilização de funçõesnão-lineares para descrição de curvas de crescimentoemovinos. Pesquisa Tecnol., 4: 1-10.

da Silva, L.S.A., Fraga, A.B., da Silva, F.D.L., Beelen, G.P.M., de Oliveira-Silva, R.M., Tonhati, H. and da Costa-Barros, C., 2010. Growth curve in Santa Inês sheep. Small Rumin. Res., 105: 182-185. https://doi.org/10.1016/j.smallrumres.2011.11.024

Daskiran, I., Kioncagul, S. and Bingol, M., 2010. Growth characteristics of indigenous Norduz female and male lambs. J. agric. Sci., 16: 62-69.

Gbangboche, A.B., Glele-Kakai, R., Salifou, S., Albuquerque, L.G. and Leroy, P., 2008. Comparison of non-linear growth models to describe the growth curve in West African Dwarf sheep. Animal, 2: 1003-1012. https://doi.org/10.1017/S1751731108002206

Geweke, J., 1992. Evaluating the accuracy of sampling-based approaches to calculating posterior moments. In: Bayesian statistics 4 (eds. J.M. Bernardo, J.O. Berger, A.P. Dawid and A.F.M. Smith). Oxford University Press, Oxford, pp. 169-193.

Goliomytis, M., Orfanos, S., Panopoulou, E. and Rogdakis, E., 2006. Growth curves for body weight and carcass components, and carcass composition of the Karagouniko sheep, from birth to 720 d of age. Small Rumin. Res., 66: 222-229. https://doi.org/10.1016/j.smallrumres.2005.09.021

Hojjati, F. and Hossein-Zadeh, N.G., 2017. Comparison of non-linear growth models to describe the growth curve of Mehraban sheep. J. appl. Anim. Res., 46: 499-504. https://doi.org/10.1080/09712119.2017.1348949

Hossein-Zadeh, N.G., 2015. Modeling the growth curve of Iranian Shall sheep using non-linear growth models. Small Rumin. Res., 130: 60-66. https://doi.org/10.1016/j.smallrumres.2015.07.014

Karakus, K., Eyduran, E., Kum, D., Ozdemir, T. and Cengiz, F., 2008. Determination of the best growth curve and measurement interval in Norduz male lambs. J. Anim. Vet. Adv., 7: 1464-1466.

Keskin, I., Dag, B., Sariyel, V. and Gokmen, M., 2009. Estimation of growth curve parameters in Konya Merino sheep. S. Afr. J. Anim. Sci., 39: 163-169. https://doi.org/10.4314/sajas.v39i2.44390

Kopuzlu, S., Sezgin, E., Esenbuga, N. and Bilgin, O.C., 2014. Estimation of growth curve characteristics of Hemsin male and female sheep. J. appl. Anim. Res., 42: 228-232. https://doi.org/10.1080/09712119.2013.842479

Kum, D., Karakus, K. and Ozdemir, T., 2010. The best nonlinear function for body weight at early phase of Norduz female lambs. Trakia J. Sci., 8: 62-67.

Laird, A.K., 1965. Dynamics of relative growth. Growth, 29: 249-263.

Lewis, R.M., Emmans, G.C., Dingwall, W.S. and Simm, G., 2002. A description of the growth of sheep and its genetic analysis. Anim. Sci. J., 74: 51-62.

Nelder, J.A., 1961. The fitting of a generalization of the logistic curve. Biometrics, 17: 89-110. https://doi.org/10.2307/2527498

Plummer, M., 2003. JAGS: A program for analysis of Bayesian graphical models using Gibbs sampling. Available at: http://citeseer.ist.psu.edu/plummer03jags.html

R Core Team, 2017. R: A language and environment for statistical computing. Available at: https://www.R-project.org/

Sieklicki, M.F., Pedrosa, V.C., Rocha, C.G., Moreira, R.P., Falcao, P.R., dos Santos, I.C., Ferreira, E.M. and Martins, A.S., 2016. Growth curves of Texel male lambs. Acta Scient. Vet., 44: 1396.

Spiegelhalter, D.J., Best, N.G., Carlin, B.P. and van der Linde, A., 2002. Bayesian measures of model complexity and fit. J. R. Stat. Soc. Ser. B., 64: 583-640. https://doi.org/10.1111/1467-9868.00353

Spiegelhalter, D.J., Thomas, A., Best, N.G. and Lunn, D., 2003. WinBUGS user manual, Version 1.4. MRC Biostatistics Unit, Cambridge.

Su, Y.S. and Yajima, M., 2015. R2jags: A Package for Running “JAGS’ from R, Version 0.05–03. R Package.

Tariq, M., Iqbal, F., Eyduran, E., Bajwa, M.A., Huma, Z.E. and Waheed, A., 2013. Comparison of non-linear functions to describe the growth in Mengali sheep breed of Balochistan. Pakistan J. Zool., 45: 661-665.

Tekel, N., Sireli, H.D., Elicin, M. and Elicin, A., 2005.Comparison of growth curve models on Awassi lambs. Ind. Vet. J., 82: 179-182.

Topal, M., Ozdemir, M., Aksakal, V., Yildiz, N. and Dogru, U., 2004. Determination of the best non-linear function in order to estimate growth in Morkaraman and Awassi lambs. Small Rumin. Res., 55: 229-232. https://doi.org/10.1016/j.smallrumres.2004.01.007

Waheed, A., Khan, M.S., Ali, S. and Sarwar, M., 2011. Estimation of growth curve parameters in Beetal goats. Arch. Tierzucht, 54: 287-296. https://doi.org/10.5194/aab-54-287-2011

Waheed, A., Eyduran, E., Tariq, M.M., Ahmad, S., Hameed, T. and Bukhari, F.A., 2016. Comparison of the non-linear models defining the growth of Thali sheep under desert conditions. Pakistan J. Zool., 48: 423-426.