New Perspectives for Predicting Growth Properties of Crayfish (Astacus leptodactylus Eschscholtz, 1823) in Uluabat Lake
New Perspectives for Predicting Growth Properties of Crayfish (Astacus leptodactylus Eschscholtz, 1823) in Uluabat Lake
Semra Benzer1,* and Recep Benzer2
1Gazi Faculty of Education, Gazi University, Teknikokullar 06500, Ankara, Turkey
2Department of Computer Engineering, National Defense University, Ankara 06654, Turkey
ABSTRACT
This study aims to compare the growth estimation result of the two methods which are Length - Weight Relations and Artificial Neural Networks from Uluabat Lake regarding narrow-clawed crayfish (Astacus leptodactylus Eschscholtz 1823) between 2015 and 2016. The relationships between total length (TL) and total weight (TW); carapace length (CL) for Astacus leptodactylus caught from Uluabat Lake were presented with tradional method of length-weight relation (LWR) Equation and Artificial Neural Networks (ANNs) method. The growth estimation of 540 crayfish was carried out with both methods and the obtained results were compared. Then, the estimated values found via both examined methods. Coefficient correlation (r2), sum square error (SSE), mean absolute percentage error performance criteria (MAPE) were used for comparison of artificial neural network and linear regression models goodness of fit. The results of the current study show that ANNs can be a superior estimation tool compared to LWR equation. Thus, as an outcome of the present study, ANNs can be considered as a finer method especially in the growth estimation of the species in biological systems. Another outcome of this study is that crayfish of Uluabat Lake well accommodates itself to the ecologic features of the environment and so its growth features are similar to the values of other water systems.
Article Information
Received 16 February 2017
Revised 27 March 2017
Accepted 18 May 2017
Available online 19 December 2017
Authors’ Contribution
SB performed the experimental work. Statistical analyses were developed by RB by using MATLAB computer software. SB and RB organized this article together.
Key words
Astacus leptodactylus, Length-weight relationship, Artificial neural networks, Crayfish.
DOI: http://dx.doi.org/10.17582/journal.pjz/2018.50.1.35.45
* Corresponding author: sbenzer@gazi.edu.tr;
sbenzer@gmail.com
0030-9923/2018/0001-0035 $ 9.00/0
Copyright 2018 Zoological Society of Pakistan
Introduction
It is well acknowledged that Astacus leptodactylus is of great element in the food webs of freshwater habitats and their examination provides advantageous information on the comprehensive water systems (Hogger, 1988; Füreder et al., 2003; Huys, 2016). The crayfish, which is examined as eutrophic water scavengers, is one of the aquatic creatures with high nutritional and economic values. Therefore, it has long attracted interests in scientific research (Holdich and Lowery, 1988). Narrow-clawed crayfish (Astacus leptodactylus), is a common species distributed throughout Europe, Middle East and Eastern Russia (Gutierrez-Yurrita et al., 1999; Souty-Grosset et al., 2006; Longshaw and Stebbing, 2016). It can be found in 27 countries around the world (Skurdal and Taugbol, 2001; Azari et al., 2015).
A. leptodactylus is naturally and widely distributed in freshwaters throughout Turkey (Harlioğlu, 2004; Harlioğlu and Harlioğlu, 2005; Aydın et al., 2015; Benzer et al., 2015; Benzer and Benzer; 2015; Demirol et al., 2015; Aksu and Harlioğlu, 2016).
Length˗weight relationships (LWR) is a widely used method, namely, in fish biology, ecology and fisheries studies. It is widely used in the determination of fishery measurement when sampling large species, mostly because of the difficulty and time required to record weight in the field (Andrade and Campos, 2002).
LWR for fish is predicted using the average length and weight (Mendes et al., 2004; Tosunoğlu et al., 2007). The LWR describes the correlation mathematically between the length and weight of the fish as well as the estimated values (Beyer, 1991) of its length and weight. LWR is beneficial for the conversion of length equations to weight for use in stock calculation models (Lindqvist and Lathi, 1983) and in predicting stock biomass with narrow sample (Verdiell˗Cubedo et al., 2006). These results also let scientists make identifications on morphological properties among species or among populations of the same species from various habitats (Etchison et al. 2012). Critically, LWR was used to inform on the condition of freshwater samples and to evaluate whether somatic growth was isometric or allometric (Ricker, 1975). The prediction of the relationship parameters between a and b can explain the connection regarding ecological events and life history. Environmental causes may affect crayfish growth by feeding and food resources. Length˗weight values may probably demonstrate the differences in growth that may be correlated with environmental stress across the species (Olsson, 2008).
The most frequently researched dimensions for crustaceans are carapace length, body length, total length, body width, and wet weight (Primavera et al., 1998). Differences in length between individual body parts are used to demonstrate the morphological changes between the male and female crayfish species (Lindqvist and Lahti, 1983). These differences are also utilized in determing crayfish populations, its relative growth, comparing the populations of the same species, the morphology of crayfish species and the systematic assignment of crayfish (Lindqvist and Lahti, 1983; Skurdal and Qvenild, 1986; Gillet and Laurent, 1995). The dimensions may be favorable to be able to convert into the desired length values when only one of the other length measurements is known and the LWR may be used to predict length from weight (Tosunoğlu et al., 2007).
Among the features and advantages of artificial neural networks (ANNs) is nonlinearity, parallelism, implemented ease of local information processing, fault tolerance, to be learned that can be system, generalization, customization, hardware acceleration, analysis and design simplicity (Öztemel, 2006). Variables in these metrics of crayfish are often non-linear or unknown. Traditional methods of statistical assay may be poor for calculation, whereas ANNs is a productive alternative way when there are non-linear patterns (Maravelias et al., 2003).
ANNs has been used in biology and in different disciplines of fisheries rather than in sciences (Tureli Bilen et al., 2011). Exercises of ANNs has included forecast the fish species distributions (Maravelias et al., 2003), fish predicting in a river (Mastrorillo et al., 1997), predicting macro invertebrate diversities (Park et al., 2003), population of aquatic insects (Obach et al., 2001), modeling freshwater fish (Joy and Death, 2004), fish population modeling (Benzer et al., 2016; Benzer and Benzer, 2016).
Compared to traditional methods, ANNs has supported better conclusions in the evaluation of future data (Suryanarayana et al., 2008; Tureli Bilen et al., 2011). For limited values, the normality and their independence from the predicted values, ANNs is asserted to be an excellent model which gives excellent predictions. ANNs is also recorded to have accomplishment compared to linear regressions (Sun et al., 2009). Besides, ANNs is more favorable for its speed and flexibility (Brosse et al., 1999).
In the present work, the LWR and ANNs for Astacus leptodactylus from varied areas were recorded, representing the deviation of the regression parameters among different locations and demonstrating as a new and alternative approach in its application in predicting the growth and weight of crayfish. Therefore, the current study provides information on the growth properties of the crayfish in Uluabat Lake in recent years, and the usefulness of ANNs approach in the growth estimation.
Materials and Methods
Study area
The study was carried out in Uluabat (Apolyont) Lake. The shallow and eutrophic Uluabat Lake is located in the western part of Turkey (40°10’ N, 28°35’ E), bordering the coastal zone of the Marmara Sea and the Kocaçay Delta basin in the north and the Emet and Orhaneli River basin in the south. Bursa, main city of the province, is approximately 30 km to the east of Uluabat Lake. The lake basin belongs partly to 4 different provinces: Bursa, Kütahya, Balıkesir and Bilecik. The lake is 22 km long and about 10.5 km wide. The water coverage of Uluabat Lake is 135 km2 (Anonymous, 2002).
Data collection
Crayfish samples were collected from Uluabat Lake. During the study, 540 crayfish specimens (270 females and 270 males) were caught between 2015 and 2016. In order to catch crayfish samples, single-entrance fyke nets, each with 34-mm mesh size, were used. The total length (TL), total weight (TW), carapace length (CL), carapace width (Cw), abdomen length (AL) and abdomen width (Aw), chela length (ChL) and chela width (Chw) of each specimen were measured. The parameters related to length and width were measured with a digital caliper to the nearest 0.1 mm, while the weight related ones were measured to the nearest 0.01 g, and sex determination was carried out for each specimen (Rhodes and Holdich, 1979). The crayfish obtained from the lake were immediately transported to the laboratory.
Length-weight relation equation
LWR equation is a traditional method used for the determination of the growth features of populations. From the collected samples; sex and length composition, the average length and weight, and the length-weight relationship for each sex and combined sexes were identified. The length-weight relationships were evaluated with the equation:
W = a Lb
Where, W stands for total body weight (g), L is the total length (mm), a and b are the coefficients of the functional regression between W and L. The equation was log transformed to estimate the parameters ‘a’ and ‘b’. When b is equal to 3, isometric pattern of growth occurs, but when b is not equal to 3, allometric pattern of growth occurs, which may be positive if >3 or negative if <3 (Ricker, 1973).
Artificial neural networks
ANNs refers to an information processing system which replicates the response of a human brain by imitating the operations and connectivity of biological neurons. As a mathematical interpretation, the ANNs result is defined as a complex nonlinear function with many parameters set to mimic the measured output in a known set of data (Lobbrecht et al., 2002). They are networks with simple processor units, interconnections, adaptive weights and scalar measurement functions (Rumelhart et al., 1986).
In an artificial neuron, the information enters the body of an artificial neuron via inputs that are individually weighed. The weighed inputs are summed and forecasted bias by the body of an artificial neuron. Then, the sum is processed with a transfer function. The artificial neuron sends the processed information via output(s) at the end. The advantage of the artificial neuron model (Krenker et al., 2011) simplicity shown with its mathematical manifestation was given below:
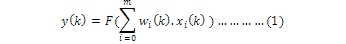
where, wi(k) is weight value in discrete time k where i goes from 0 to m, xi(k) is input value in discrete time k where i goes from 0 to m, F is a transfer function and yi(k) is output value in discrete time k.
As it is clear in the model of an artificial neuron and its equation (1), the major unknown variable of this model is its transfer function which identifies the features of artificial neuron and can be any mathematical function.
During the training of the network, the input data and the input-output relationship between the learning of the network is provided. This method, which is generally called supervised learning, is one of the preferred methods (Haykin, 1999). The supervised learning method trained with the network structure (back-propagation networks) will be used to solve problems in this study.
The transfer function (2), mostly used a sigmoid or a logistic function, gives values in the range of [0,1] and can be described as (normalization):
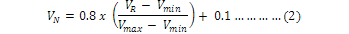
where, VN is normalized data, VN is data to be normalized, Vmin is minimum value of the data and Vmax is maximum value of the data.
This study used the sigmoid activation function. ANNs can work with a small data set; and it seems better than other methods because it has such significant features as generalization, learning from data, working with unlimited number of variables and no need for any information about the problem in advance.
Sum squared error (SSE) and mean absolute percentage error (MAPE) were used as the two performance criteria. SSE was used as convergence criteria during the training of the network. Comparisons can be made with more than one method by MAPE, because it is easy to interpret with its relative measurements. The smaller the values of MAPE, the closer are the forecasted values to the actual values.
SSE and MAPE are described by equations 3 and 4, respectively.
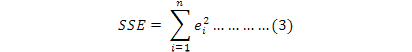
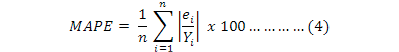
where, Yi is the actual observation value, ei is the difference between the actual value and prediction value and n is the number of total observations.
Neural Network Toolbox of MATLAB (Ver R2015b) was used for the ANNs calculations. This study was performed on 540 crayfish (270 females and 270 males) caught between 2015 and 2016 in Uluabat Lake. The data were divided into three equal parts: training, validation and test sets. The MATLAB functions were used for “training”, “testing” and “validation”. They were used randomly; 70% in training, 15% in testing, and 15% in the validation of the crayfish.
Statistics
The correlation coefficient r was used to measure the strength and direction of the linear relationship between the two variables on the distribution line. Correlation is an effect size and so the strength of the correlation using the guide that Evans (1996) suggests for the absolute value of r (very weak: 0.00-0.19; weak: 0.20-0.39; medium: 0.40-0.59; strong: 0.60-0.79; very strong: 0.80-1.0) was described. Variables were reported as Mean ± Sx. Means were compared using the t-test (Hald, 1952; Panofsky and Brier, 1968). Statistical analyses were performed using SPSS software (SPSS Inc., USA). The significance level was set at 0.05.
Table I.- Some metric properties for crayfish.
| Metric species | Sex |
Median ± Sx |
Min-Max |
t test |
| TL |
♀ ♂ ♀♂ |
11.87± 1.64 11.78± 1.64 11.83.± 1.64 |
9.5-15.3 9.7-14.5 9.5-15.3 |
P<0.05 |
| TW |
♀ ♂ ♀♂ |
40.86± 16.28 45.43± 19.85 43.16± 18.29 |
14.99-79.02 18.87-88.54 14.99-88.54 |
P<0.05 |
| CL |
♀ ♂ ♀♂ |
5.69± 0.86 5.98± 1.02 5.84± 0.96 |
4.5-7.4 4.5-7.5 4.5-7.5 |
P<0.05 |
| AL |
♀ ♂ ♀♂ |
6.18± 0.81 5.80± 0.66 5.99±0.76 |
4.9-8.0 4.7-7.0 4.7-8.0 |
P<0.05 |
| ChL |
♀ ♂ ♀♂ |
7.35±1.21 9.54±2.74 8.45±2.39 |
4.5-9.8 6.0-14.70 4.5-14.70 |
P<0.05 |
| Cw |
♀ ♂ ♀♂ |
2.99±0.59 2.99±0.68 2.99±0.64 |
2.0-4.4 2.0-4.8 2.0-4.8 |
P<0.05 |
| Aw |
♀ ♂ ♀♂ |
2.21±0.42 1.96±0.38 2.08±0.42 |
1.5-3.5 1.2-2.5 1.2-3.5 |
P<0.05 |
| Chw |
♀ ♂ ♀♂ |
1.54±0.33 1.91±0.67 1.73±0.56 |
0.70-2.5 1.0-4.3 0.7.4.3 |
P<0.05 |
Sx, standard error; TW, total weight; Cw, carapace width; CL, carapace length; Chw, chela width; ChL, chela length; TL, total length; AL, abdomen length; Aw, abdomen width; ♀, female; ♂, male; ♀♂, female+male
Table II.- Some metric ratio for crayfish.
| Metric ratio | Sex |
Average ± Sx |
Min-Max | t test |
| CL/TL |
♀ ♂ ♀♂ |
0.48 ± 0.01 0.51 ± 0.02 0.49 ± 0.02 |
0.45 – 0.52 0.46 – 0.53 0.45 – 0.54 |
P < 0.05 |
| Cw/CL |
♀ ♂ ♀♂ |
0.53 ± 0.06 0.50 ± 0.05 0.51 ± 0.06 |
0.43 – 0.71 0.40 – 0.64 0.40 - 0.71 |
P < 0.05 |
| AL/TL |
♀ ♂ ♀♂ |
0.52 ± 0.01 0.49 ± 0.02 0.51 ± 0.02 |
0.49 – 0.55 0.46 – 0.56 0.46 – 0.56 |
P < 0.05 |
| Aw/AL |
♀ ♂ ♀♂ |
0.36 ± 0.04 0.34 ± 0.45 0.35 ± 0.04 |
0.29 – 0.46 0.22 – 0.48 0.22 – 0.48 |
P < 0.05 |
| CL/Al |
♀ ♂ ♀♂ |
0.92 ± 0.05 1.03 ± 0.09 0.97 ± 0.09 |
0.82 – 1.05 0.80 – 1.15 0.80 – 1.15 |
P < 0.05 |
| Aw/Cw |
♀ ♂ ♀♂ |
0.75 ± 0.09 0.67 ± 0.09 0.71 ± 0.10 |
0.56 – 1.00 0.50 – 0.95 0.50 – 1.00 |
P < 0.05 |
| Chw/ChL |
♀ ♂ ♀♂ |
0.21 ± 0.04 0.20 ± 0.06 0.21 ± 0.05 |
0.14 – 0.42 0.14 – 0.50 0.14 – 0.50 |
P < 0.05 |
For abbreviations and details of symbols, see Table I.
Results
There were about 50 % female and 50 % male crayfish. The female: male ratio was found to be 1:1 for the general population (Abrahamsson, 1971). The length and weight (min-max) of the crayfish were 95– 153 mm and 14.99 – 88.54 g. The average length (mm) and weight (g) of samples were 11.78 ± 1.64 and 45.43 ± 19.85 for the male, 11.87 ± 1.64 and 40.86 ± 16.28 for the females and 11.83 ± 1.64 and 43.16 ± 18.29 for the combined sex, respectively (Table I). Total weight (TW), carapace width (Cw), carapace length (CL), chela width (Chw), chela length (ChL) of the females were lower than the males, while Total length (TL) and abdomen length (AL), abdomen width (Aw) of the females were higher than the males (Table I). TL, TW, CL, Cw, AL, Aw, ChL and Chw of the females and the males were insignificant (p < 0.05).
CL/TL, Cw/CL, AL /TL, Aw/AL, CL /AL, Aw /Cw and Chw/ChL ratio results of crayfish were shown in Table II. They were insignificant (p < 0.05). CL/TL and CL/AL of the males were higher than the females (Table II). There are very strong correlations between TW - TL, CL - TL, AL - TL, CL - TW, AL - TW, ChL - TW, AL - CL, ChL - CL, Aw - TL in the present study (Table III).
Table III.- Pearson correlation coefficients between metric properties.
| TL | TW | CL | AL | Aw | ChL | Chw | |
| TL | 1.000 | ||||||
| TW |
0.920* |
1.000 | |||||
| CL |
0.965** |
0.929* |
1.000 | ||||
| AL |
0.944* |
0.817* |
0.824* |
1.000 | |||
| Aw |
0.794* |
0.700* |
0.726* |
0.799* |
1.000 | ||
| ChL |
0.739* |
0.818** |
0.826* |
0.550* |
0.517* |
1.000 | |
| Chw |
0.419* |
0.538* |
0.493* |
0.284* |
0.266* |
0.487* |
1.000 |
*Correlation is significant at 0.01 level; For abbreviations, see Table I.
The total length – total weight relations (TL - TW) for the crayfish in Uluabat Lake were found as W = 0.04059605 L2.7750 for the females, W = 0.02999258 L 2.9479 for the males and W = 0.03634341 L2.8450 for the females+males. The carapace length – total length relations (CL - TL) for the crayfish in Uluabat Lake were found as W= 2.52734198 L0.8898 for the females, W = 2.90296047 L0.7842 for the males and W = 2.82720404 L0.8118 for the females+males. The chela length–total length relations (ChL - TL) for the crayfish in Uluabat Lake were found as W=3.19630403 L0.6533 for the females, W = 4.46302404 L0.4339 for the males and W = 5.14611909 L0.389 for the females+males.
Table IV.- Length-weight relation parameters, equations and correlation coefficients.
| Species | Sex | Relationship |
r2 |
| TL – TW |
♀ ♂ ♀♂ |
W = 0.04059605 L 2.7750 W = 0.02999258 L 2.9479 W = 0.03634341 L 2.8450 |
0.968 0.959 0.961 |
| CL – TL |
♀ ♂ ♀♂ |
W = 2.52734198 L 0.8898 W = 2.90296047 L 0.7842 W = 2.82720404 L 0.8118 |
0.998 0.999 0.999 |
| ChL – TL |
♀ ♂ ♀♂ |
W = 3.19630403 L 0.6533 W = 4.46302404 L 0.4339 W = 5.14611909 L 0.389 |
0.996 0.987 0.980 |
| AL – TL |
♀ ♂ ♀♂ |
W = 1.75284306 L 1.0501 W = 1.53328189 L 1.1584 W = 1.84379994 L 1.0374 |
0.999 0.998 0.999 |
For abbreviations and details of symbols, see Table I.
The abdomen length - total length relations (AL - TL) for the crayfish in Uluabat Lake were found as W= 1.75284306 L1.0501 for the females, W = 1.53328189 L 1.1584 for the males and W = 1.84379994 L1.0374 for the females+males (Fig. 1, Table IV).
A multilayer feed-forward neural network was used for the ANNs. A schematic representation of a typical ANNs was shown in Figure 2. Figure 3 illustrates graphical presentation of the fit between the actual and predicted values. Performance of the ANNs between forecast values for TL TW was seen in Figure 4.
The observed data with gender, length and weight, and the values calculated with both ANNs and LWR were presented in Table V. Table V was provided for the comparison of the data of the crayfish in Uluabat Lake.
Table V shows the regression and ANN values and the MAPE values calculated using the samples taken from the nature. It has been determined that the ANNs MAPE
Table V.- Observed and calculated values for ANNs and LWR.
| Type (1) - (2) | Gender |
Naturel environment (Uluabat Lake) |
ANNs calculate MATLAB |
MAPE (%) |
Regression relations |
MAPE (%) |
||||||
|
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
|||
|
Total body length (1) Body weight (2) |
♀ |
11.85 |
40.86 |
11.59 |
43.01 |
2.18 |
5.28 |
12.08 |
38.73 |
1.94 |
5.20 |
|
| ♂ |
11.73 |
45.43 |
11.47 |
42.81 |
2.21 |
5.75 |
11.99 |
42.57 |
2.22 |
6.28 |
||
| ♀♂ |
11.79 |
43.16 |
11.48 |
42.89 |
2.65 |
0.64 |
12.14 |
40.62 |
3.01 |
5.89 |
||
|
Carapace length (1) Total body length (2) |
♀ |
5.68 |
11.85 |
5.73 |
11.94 |
0.87 |
0.77 |
5.68 |
11.86 |
0.09 |
0.08 |
|
| ♂ |
5.95 |
11.73 |
5.85 |
11.74 |
1.58 |
0.10 |
5.93 |
11.72 |
0.25 |
0.06 |
||
| ♀♂ |
5.82 |
11.79 |
5.75 |
11.94 |
1.12 |
1.31 |
5.92 |
11.92 |
1.73 |
1.07 |
||
|
Chela length (1) Total body length (2) |
♀ |
7.44 |
11.85 |
8.09 |
11.73 |
8.74 |
1.06 |
7.43 |
11.86 |
0.07 |
0.05 |
|
| ♂ |
9.61 |
11.73 |
8.79 |
11.72 |
8.51 |
0.07 |
9.42 |
11.83 |
1.98 |
0.87 |
||
| ♀♂ |
8.53 |
11.79 |
8.39 |
11.73 |
1.68 |
0.62 |
8.34 |
11.89 |
2.42 |
0.92 |
||
|
Abdomen length (1) |
♀ |
6.17 |
11.85 |
6.10 |
11.83 |
1.11 |
0.29 |
6.17 |
11.84 |
0.07 |
0.07 |
|
| ♂ |
5.78 |
11.73 |
5.88 |
11.79 |
1.78 |
0.53 |
5.79 |
11.71 |
0.18 |
0.21 |
||
| ♀♂ |
5.97 |
11.79 |
5.99 |
11.80 |
0.28 |
0.09 |
6.10 |
11.75 |
2.13 |
0.29 |
||
|
|
1.43 |
0.67 |
|
2.32 |
2.04 |
|||||||
For abbreviations and details of symbols, see Table I.
values in TL-TW and ChL-TL are better than MAPE values calculated in relation to regression. In the CL-TL and AL-TL relationship, the MAPE values of the regression relation were found to be better than the ANNs MAPE values.
Dıscussıon
Environmental factors such as behavior, foraging efficiency, feeding and the availability and quality of food resources might widely influence variation in morphometric traits (Lindqvist and Lahti, 1983). Crustacean growth is affected by the environmental conditions by influencing molt intervals and incremental rises in length and weight. In fishery studies, the relationship between bodies length - weight is an essential and extensively used equation and the simplest parameter to measure is the fish length. Crustaceans experience different stages in their life history which are defined by different length˗weight relationships. The parameter b is characteristic of species and usually does not show a significant change throughout the year, unlike the parameter, which may change on a daily basis, seasonally, between different environments, water temperature and salinity, gender, availability of food, diversity in the number of specimens analyzed, as well as in the observed length ranges of the species caught (Tesch, 1971).
The morphological differences are used in determining the growth characteristics of the freshwater crayfish population, comparing populations of the same species with different regions and classifying freshwater crayfish systematically (Harlioğlu, 1999).
The numbers of the males were equal to the females in Uluabat Lake in this research. Some researchers reported that the number of males were higher than females (Berber and Balık, 2009; Deniz et al., 2013; Benzer et al., 2015; Benzer and Benzer, 2016; Aydın et al., 2015) while some researchers reported the opposite in their locations of study (Harlioğlu, 1999; Harlioğlu and Harlioğlu, 2005) (Table VI).
The average lengths of the females were higher than the males while the average weight of the males was higher than that of females in this study. It was found that TL of all sex was longer than that of all the literature (Table VI). Some researchers have indicated that the females have a larger size than the males (Benzer et al., 2015; Aydın et al., 2015; Balık et al., 2005; Berber and Balık, 2006), while some researchers have indicated that male females are longer than female females (Harlioğlu, 1999; Berber and Balık, 2009; Benzer and Benzer, 2016).
In some studies, it is stated that females are heavier than males (Berber and Balık, 2006; Aydın et al., 2015), and some studies indicate that males are heavier than females (Benzer et al., 2015; Benzer and Benzer, 2016; Balık et al., 2005; Berber and Balık, 2009).
The slope (b) values of the length–weight relationship in both genders were found as 2.845. In the present study, growth was a negative allometry for the females and males. It was found that b values were lower than the values found in the study by Harlioğlu (1999), Harlioğlu and Harlioğlu (2005) (Eğirdir and İznik Lake), Benzer et al. (2015). It was found that b values were higher than the values found in the study by Balık et al. (2005), Berber and Balık (2006), (2009), Deniz et al. (2013) and Aydın et al. (2015) (Table VI).
The differences may result from the environmental factors, food, density of the population and the selectivity of the traps or fykenets used in the studies. For example, male crayfish were found heavier than females in a previous study. This disparity is said to be a result of the increasing development of the male chela with sexual maturity; however, the chela of the females remain isometric during their life (Romaire et al., 1977). Furthermore, males were found rougher and more thick-set than females in another study (Skurdal and Qvenild, 1986).
Table VI.- Comparison of crayfish parameters in different locations.
| Referee | Sex |
TL |
TW |
Regression parameters |
Sex ratio (F/M) |
||
|
a |
b |
r2 |
|||||
|
Keban Dam Lake |
♀ ♂ |
106.79 108.14 |
- |
0.00159 0.00093 |
2.52 2.67 |
0.88 0.92 |
1.16:1 |
|
Harlioğlu and Harlioğlu (2005) Eğirdir Lake İznik Lake Hirfanli Dam Lake |
♀ ♂ |
103.29 101.81 |
32.17 33.07 |
- |
2.11 2.51 |
0.82 0.92 |
1.14:1 |
|
♀ ♂ |
104.54 100.47 |
29.19 29.34 |
- |
2.66 2.72 |
0.94 0.94 |
1.15:1 |
|
|
♀ ♂ |
105.93 104.76 |
19.36 20.17 |
- |
2.22 3.66 |
0.78 0.89 |
0.82:1 |
|
|
Demirköprü Dam Lake |
♀ ♂ |
92.88 90.18 |
24.19 25.43 |
0.00002 0.00001 |
3.06 3.27 |
0.97 0.98 |
0.49:1 |
|
Manyas Lake |
♀ ♂ |
89.07 82.12 |
21.85 19.57 |
0.0003 0.0003 |
2.94 2.98 |
0.99 0.97 |
|
|
Apolyont Lake |
♀ ♂ |
- |
20.62 21.92 |
0.0003 0.0002 |
2.96 3.03 |
0.94 0.95 |
0.68:1 |
|
Inland water in Turkey Eğirdir Lake Hirfanli Dam Lake Keban Dam Lake Porsuk Dam Lake |
♀ ♂ |
- |
- |
0.00003 0.00003 |
2.96 2.97 |
0.87 0.88 |
0.84:1 |
|
♀ ♂ |
- |
- |
0.00007 0.00001 |
2.78 3.21 |
0.88 0.93 |
0.91:1 |
|
|
♀ ♂ |
- |
- |
0.0001 0.000008 |
2.71 3.28 |
0.90 0.92 |
0.57:1 |
|
|
♀ ♂ |
- |
- |
0.0001 0.000005 |
2.42 3.38 |
0.75 0.83 |
0.87:1 |
|
|
Mogan Lake |
♀ |
108.71 |
28.64 |
0.00220024 |
2.021 |
0.99 |
0.14:1 |
| ♂ |
102.93 |
32.49 |
0.00095247 |
2.229 |
0.99 |
||
|
Dikilitaş Pond |
♀ ♂ |
110.6 113.5 |
38.52 50.02 |
0.03105469 0.05958618 |
2.98 2.76 |
0.98 0.99 |
0.68:1 |
|
İznik Lake |
♀ ♂ |
104.17 95.71 |
32.50 28.82 |
0.00003 0.000008 |
3.01 3.30 |
0.97 0.97 |
0.89:1 |
| This study |
♀ ♂ ♀♂ |
118.72 117.80 118.26 |
40.86 45.43 43.16 |
0.04059605 0.02999258 0.03634341 |
2.775 2.947 2.845 |
0.968 0.959 0.961 |
1:1 |
For abbreviations and details of symbols, see Table I.
The relationships between carapace length and weight can be used for various purposes. For example, in order to calculate biomass and to predict the recovery of edible meat of crayfish in different sizes, these relationships can be used as the indicators of condition. In the study of crustaceans; however, body weight and total length, carapace length and carapace width are the most commonly used dimensions (Atar and Seçer, 2003). The assessment of the dimensions mentioned above can be utilized in the determination of the different growth rates between sexes.
The estimated length-weight relations are model dependent, so in some data sets the uncertainty of model selection can be quite high. Neglecting model selection uncertainty may result in considerable overestimation of the precision and estimation of the confidence intervals of the criterion below the nominal level. This uncertainty has significant indications, such as the comparisons of the growth parameters of different crayfish populations (Benzer et al., 2015).
Statistical calculations such as the determination coefficient correlation (r2), sum square error (SSE) and mean absolute percentage error performance criteria (MAPE) were used to test the performance of developed ANNs.
The MAPE criterion refers to estimation errors as a percentage, and can therefore negate the disadvantages that may arise when comparing models developed for studies with different unit values. These features of MAPE are considered to be superior to those of other evaluation statistics. Models with MAPE values less than 10% are classified as “high accuracy” and models with 10% to 20% are classified as accurate estimators (Witt and Witt, 1992). Similarly, Lewis (1982) categorized models with a MAPE value of less than 10% as “very good” in estimating, 10% to 20% as “good”, 20% to 50% as “acceptable” and over 50% are classified as “wrong and faulty” models.
The TL - TW relationship, which shows the estimate power of the developed ANNs, was found to be 0.964 as the r2 (for all individuals) values. Success is considered high when r2 values are between 0.95-1 (Ekici and Aksoy 1993). The calculated SSE value for ANNs was calculated as 488.248 and 53802.950 for length and weight of crayfish.
The coefficient correlation (r2) calculated by the LWR regression model (for all individuals) was 0.961. The SSE value for LWR was found to be 552.276 and 59272.368 for length and weight. When the coefficient correlation (r2) was evaluated in both ANNs and LWL model, the results of ANNs were better, although they did not seem close to each other. It is evaluated that comparing the MAPE values together with r2 and SSE values can give a healthy result (Gentry et al., 1995).
When MAPE results of length-weight relation and ANNs were compared, it was found that MAPE value of the forecast of ANNs was 1.431 and 0.667, and the value of length-weight relationship was 2.323 and 2.042 for length–weight of all genders. As seen in Table III, ANNs gives better results than length-weight relation. In the literature, it is reported that ANNs MAPE ratios are low (Tureli Bilen et al., 2011; Benzer and Benzer, 2016; Benzer et al., 2015, 2016).
As seen in Table V, ANNs gives better results than LWR. The comparative study conducted between ANNs and LWR models on the growth that all the models show high accurate estimation, with ANNs model as the best one. Therefore, it was possible to substantiate once again the fact that ANNs models constitute a technique to be taken into account by researchers and in forecasting of fisheries.
According to all these considerations, high r2 and low MSE, MAPE valued model is considered as a good model. Thus, it is seen that ANNs has a higher rate of accurate prediction than the regression analysis and give fewer false results. It can be concluded that the ANNs has relatively high potential for predicting the length-weight of crayfishes. In conclusion, the use of ANNs as a forecasting tool was found to achieve high performance in the present study.
Conclusıons
The morphometric characteristics can be a useful element in the comparison of the same species in different places and it could be used in the description of populations. This study also provides information on the length˗weight relationships that would be useful for sustainable management of fisheries in Uluabat Lake. Finally, it is recommended that the crayfish population should be carefully monitored in the future to ensure sustainable economic yield.
Acknowledgments
We would like to express our gratitude to the referees for their help and support to our research with their reviews and recommendations. This study has been accepted for oral presentation at International Symposium on Fisheries and Aquatic Sciences in 2015 (FABA 2016, Antalya, Turkey).
Statement of conflict of interest
Authors have declared no conflict of interest.
REFERENCES
Abrahamsson, S.A.A., 1971. Density, growth and reproduction in populations of Astacus astacus and Pacifastacus lenisculus in isolated pond. Oıkos, 22: 373-380. https://doi.org/10.2307/3543861
Aksu, Ö. and Harlioğlu, M.M., 2016. The effect of placing hides into the natural habitat on Astacus leptodactylus (Eschscholtz, 1823) harvest. Ecol. Life Sci., 11: 1-10. https://doi.org/10.12739/nwsa.2016.11.2.5a0077
Andrade, H.A. and Campos, R.O., 2002. Allometry coefficient variations of the length-weight relationship of skipjack tuna (Katsuwonus pelamis) caught in the southwest South Atlantic. Fish. Res., 55: 307-312. https://doi.org/10.1016/S0165-7836(01)00305-8
Anonymous, 2002. Masterplan Draft for Lake Uluabat. Turkey Ministry for Environment, İstanbul.
Atar, H.H. and Seçer, S., 2003. Width/length˗weight relationships of the blue crab (Callinectes sapidus Rathbun 1896) population living in Beymelek Lagoon Lake. Turk. J. Vet. Anim. Sci., 27: 443˗447.
Aydin, H., Harlioğlu, M.M. and Deniz, T., 2015. An investigation on the population parameters of freshwater crayfish (Astacus leptodactylus Esch., 1823) in Lake İznik (Bursa). Turk. J. Zool., 39: 660-668. https://doi.org/10.3906/zoo-1406-6
Balık, S., Ustaoğlu, M.R., Sarı H.M. and Berber, S., 2005. Determination of traits some growth and morphometric of crayfish (Astacus leptodactylus Eschscholtz, 1823) at Demirköprü Dam Lake (Manisa). E.U. J. Fish. aquat. Sci., 22: 83-89.
Benzer, S. and Benzer, R., 2015. Determine some morphological characteristics of crayfish (Astacus Leptodactylus Eschscholtz, 1823) with tradional methods and artificial neural networks in Dikilitas Pond, Ankara, Turkey. Fresenius environ. Bull., 24: 3727-3735.
Benzer, S., Karasu-Benli, Ç. and Benzer, R., 2015. The comparison of growth with length-weight relation and artificial neural networks of crayfish, Astacus leptodactylus, in Mogan Lake. J. Black Sea/Mediterr. Environ., 21: 208-223.
Benzer, S. and Benzer, R., 2016. Evaluation of growth in pike (Esox lucius L., 1758) using traditional methods and artificial neural networks. Appl. Ecol. environ. Res. 14: 543-554. https://doi.org/10.15666/aeer/1402_543554
Berber, S. and Balık, S., 2006. Determination of traits some growth and morphometric of crayfish (Astacus leptodactylus Eschscholtz, 1823) at Manyas Lake (Balıkesir). E.U. J. Fish. aquat. Sci., 23: 83-91.
Berber, S. and Balık, S., 2009. The length-weight relationships, and meat yield of crayfish (Astacus leptodactylus Eschcholtz, 1823) population in Apolyont Lake (Bursa, Turkey). J. Fish. Sci., 3: 86-99.
Beyer, J.E., 1991. On length˗weight relationships: Part II. Computing mean weights from length statistics. Fishbyte, 9: 50˗54.
Brosse, S., Guegan, J., Tourenq, J. and Lek, S., 1999. The use of artificial neural networks to assess fish abundance and spatial occupancy in the littoral zone of a Mesotrophic lake. Ecol. Model, 120: 299-311. https://doi.org/10.1016/S0304-3800(99)00110-6
Demirol, F., Gündüz, F., Yüksel, F., Çoban, M.Z., Abdulmutalip, B.E.R.İ., Kurtoğlu, M. and Küçükyilmaz, M., 2015. The ınvestigation of by-catch and discard rates in crayfish (Astacus leptodactylus Eschscholtz, 1823) catching in the Keban Dam Lake. J. Limnol. Freshw.Fish. Res., 1: 69-74. https://doi.org/10.17216/LimnoFish-5000128537
Ekici, B.B. and Aksoy, U.T., 1993. Prediction of building energy consumption by using artificial neural networks. Adv. Engin. Softw., 40: 356-362. https://doi.org/10.1016/j.advengsoft.2008.05.003
Evans, J.D., 1996. Straightforward statistics for the behavioral sciences. Brooks/Cole Publishing, Pacific Grove, CA.
Füreder, L., Oberkofler, B., Hanel, R., Leiter J. and Thaler, B., 2003. The freshwater crayfish Austropotamobius pallipes in South Tyrol: Heritage species and bioindicator. Bull. Fr. Peche Piscic, 370-371: 79-95. https://doi.org/10.1051/kmae:2003005
Gillet, C. and Laurent, P.J., 1995. Tail length variations among noble crayfish (Astacus astacus (L)) populations. Freshw. Crayfish, 10: 31-36.
Gutiérrez-Yurrita, P.J., Martínez, J.M., Bravo-Utrera, M.A., Montes, C., Ilhéu M. and Bernardo, J.M., 1999. The status of crayfish populations in Spain and Portugal. İn: Crayfish in Europe as alien species: How to make the best of a bad situation? (eds. F. Gherardi and D.M. Holdich). A.A. Balkema, Rotterdam, Netherlands, pp. 161-192.
Hald A., 1952. Statistical theory with engineering applications. Wiley: New York. pp. 571.
Harlioğlu, M.M., 1999. The relationships between length-weight, and meat yield of freshwater crayfish, Astacus leptodactylus Eschscholtz, in the Ağın Region of Keban Dam Lake. Turk. J. Zool., 23: 949-958.
Harlioğlu, M.M., 2004. The present situation of freshwater crayfish, Astacus leptodactylus (Eschscholtz, 1823) in Turkey. Aquaculture, 230: 181-187. https://doi.org/10.1016/S0044-8486(03)00429-0
Haykin, S., 1999. Neural networks: A comprehensive foundation. Perenctice Hall, New Jersey.
Huys, R., 2016. Harpacticoid copepods-their symbiotic associations and biogenic substrata: A review. Zootaxa, 4174: 448-729. https://doi.org/10.11646/zootaxa.4174.1.28
Holdich, D.M. and Lowery, R.S., 1988. Freshwater crayfish - Biology, management and exploitation. Chapman and Hall, London, pp.498.
Joy, K.M. and Death, R.G., 2004. Predictive modelling and spatial mapping of freshwater fish and decapod assemblages using GIS and neural Networks. Freshw. Biol., 49: 1306-1052. https://doi.org/10.1111/j.1365-2427.2004.01248.x
Lewis, C.D., 1982. Industrial and business forecasting methods. Butterworths, London.
Lindqvist, O.V. and Lahti, E., 1983. On the sexual dimorphism and condition index in the crayfish Astacus astacus L. in Finland. Freshw. Crayfish, 5: 3-11.
Lobbrecht, A.H., Dibike, Y.B. and Solomatine, D.P., 2002. Applications of neural networks and fuzzy logic to ıntegrated water management. Project Report, pp. 173.
Longshaw, M. and Stebbing, P., 2016. Biology and ecology of crayfish. CRC Press, Taylar and Francis Group, pp. 375. https://doi.org/10.1201/b20073
Maravelias, C.D., Haralabous, J. and Papaconstantinou, C., 2003. Predicting demersal fish species distributions in the Mediterranean Sea using artificial neural networks. Mar. Ecol., 255: 249-258. https://doi.org/10.3354/meps255249
Mastrorillo, S., Lek, S., Dauba, F. and Belaud, A., 1997. The use of artificial neural networks to predict the presence of small-bodied fish in river. Freshw. Biol., 38: 237-246. https://doi.org/10.1046/j.1365-2427.1997.00209.x
Mendes, B., Fonseca, P. and Campos, A., 2004. Weight length relationships for 46 fish species of the Portuguese west coast. J. appl. Ichthyol., 20: 355-361. https://doi.org/10.1111/j.1439-0426.2004.00559.x
Obach, M., Wagner, R., Werner, H. and Schmidt, H.H., 2001. Modelling population dynamics of aquatic insects ith artificial neural networks. Ecol. Model., 146: 207-217. https://doi.org/10.1016/S0304-3800(01)00307-6
Öztemel, E., 2006. Artificial neural networks. Papatya Press, İstanbul.
Panofsky, H.A. and Brier G.W., 1968. Some applications of statistics to meteorology. Pennsylvania State University, University Park, pp. 224.
Park, Y.S., Verdonschot, P.F.M., Chon, T.S. and Lek, S., 2003. Patterning and predicting aquatic macro invertabrate diversities using artificial neural network. Water Res., 37: 1749-1758. https://doi.org/10.1016/S0043-1354(02)00557-2
Primavera, J.H., Parado-Estepa, F.D. and Lebata, J.L., 1998. Morphometric relationship of length and weight of giant tiger prawn Penaeus monodon according to life stage, sex and source. Aquaculture, 164: 67–75. https://doi.org/10.1016/S0044-8486(98)00177-X
Rhodes, C.P. and Holdich, D.M., 1979. On size and sexual dimorphism in Austropotamobius pallipes (Lereboullet) - A step in assessing the commercial exploitation potential of the native British freshwater crayfish. Aquaculture, 17: 345-358. https://doi.org/10.1016/0044-8486(79)90089-9
Ricker, W.E., 1973. Linear regressions in fishery research. J. Fish. Res. Bd. Can., 30: 409-434. https://doi.org/10.1139/f73-072
Romaire, R.P., Forester J.S. and Avault, J.W., 1977. Length˗weight relationships of two commercially important crayfishes of the genus Procambarus. Freshw. Crayfish, 3: 463˗470.
Rumelhart, D.E., Hinton, G.E. and Williams, R.J., 1986. Learning internal representations by error propagation in parallel distributed processing. Explor. Microstruc. Cognition, MIT Press, 1: 318-362.
Skurdal, J. and Qvenild, T., 1986. Growth, maturity, and fecundity of Astacus astacus in lake Steinfjorden, S.E. Norway. Freshw. Crayfish, 6: 182-186.
Skurdal, J. and Taugbol, T., 2001. Crayfish of commercial importance-Astacus. In: Biology of freshwater crayfish (ed. D.M. Holdich). Blackwell Science, Oxford, pp. 467–510.
Souty-Grosset, C., Holdrich, D.M., Noel, P.Y., Reynolds, J.D. and Haffner, P., 2006. Atlas of crayfish in Europe. Publications Scientifiques du MNHN-Paris.
Sun, L., Xiao, H., Li, S. and Yang, D., 2009. Forecating fish stock recruitment and planning optimal harvesting strategies by using neural network. J. Comput., 4: 1075-1082.
Suryanarayana, I., Braibanti, A., Rao, R.S., Ramamc, V.A., Sudarsan, D. and Rao, G.N., 2008. Neural networks in fisheries research. Fish. Res., 92: 115-139. https://doi.org/10.1016/j.fishres.2008.01.012
Tosunoğlu, Z., Aydın, C., Özaydın, O. and Leblebici, S., 2007. Trawl codend mesh selectivity of braided PE material for Parapenaeus longirostris (Lucas, 1846) (Decapoda, Penaeidae). Crustaceana, 80: 1087-1094. https://doi.org/10.1163/156854007782008649
Verdiell-Cubedo, D., Oliva-Paterna, F.J. and Torralva, M., 2006. Length-weight relationships for 22 fish species of the Mar Menor coastal lagoon (Western Mediterranean Sea). J. appl. Ichthyol., 22: 293-294. https://doi.org/10.1111/j.1439-0426.2006.00738.x
Witt, S.F. and Witt, C.A., 1992. Modeling and forecasting demand in tourism. Academic Press, Londra.