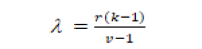New Diallel Cross Designs Through Resolvable Balanced Incomplete Block Designs for Field Experiments

Research Article

New Diallel Cross Designs Through Resolvable Balanced Incomplete Block Designs for Field Experiments

Ijaz Iqbal 1, Maqsooda Parveen1 and Zafar Mahmood2*

1Department of Statistics, Bahauddin Zakariya University Multan, Pakistan; 2Department of Maths, Stats and Computer Science, UAP, Pakistan.

Received | May 17,2018; Accepted |November 11, 2018; Published | November 29, 2018

*Correspondence | Zafar Mahmood, Department of Maths, Stats and C. Science, UAP, Pakistan; Eamil: zafarjan@aup.edu.pk

Citation | Iqbal, I., M. Parveen and Z. Mahmood. 2018. New diallel cross designs through resolvable balanced incomplete block designs for field experiments. Sarhad Journal of Agriculture, 34(4): 994-1000.

DOI | http://dx.doi.org/10.17582/journal.sja/2018/34.4.994.1000

Keywords | Experimental design, Cyclic shifts, Balanced incomplete block design, Resolvable design, Diallel cross design

Introduction

Schmidt (1919) was the great innovator of the term diallel. However, in this case we are dealing with Griffing (1956) method. In two fields, e.g. in plant and animal breeding, the modern use of diallel cross started with the development of the idea of general combining ability(gca) and specific combining ability (sca) originated by Sprague and Tatum (1942). Although most of the work have done in the field of design for factorial experiments and varietal trials, but it was not much development in diallel cross experiment design, for more detailed study these articals; Gupta and Kageyama (1994), Dey and Midha (1996), Mukerjee (1997), Das et al. (1998), Kageyama (1998), Bailey et al. (1995). Iqbal et al. (2009), Iqbal et al. (2012), Labdi et al. (2015), Harriman and Nwammadu (2016), Antoine et al. (2017), Okoro and Mbajiorgu (2017) and many others have done work in the same type of designing. The analysis of diallel cross design based on a fixed effect model for diallel analysis which is proposed by Hayman (1954).

In block designs, the combinatorial study of resolvability have existed since a time in the past and approaches to the well-known work by Craigen and Kharaghani (2007). Most of the work done on resolvable design by different author e.g. Reck (2002), Sinha (1978), Mukerjee and Kageyama (1985), Ge et al. (2008), Abel (2001) etc. A large family of resolvable designs was introduced by Williams(1975), Patterson and Williams (1976), which they denoted as α-designs. Williams et al. (1976) developed resolvable designs with two replacements from balanced incomplete block (BIB) designs. Baily et al. (1995) constructed affine resolvable design for replicate r ≥ 3 whenever the square of the block size properly divided by the number of treatments. Pseudo factors were used to analyze the data.

Resolvable BIB designs have attained noteworthy interest in the statistical and the combinatorial literature together. In a nutshell, see Morgan (1996), who discussed the key modules of resolvable designs in lots of orientations. With α-designs, Patterson and Williams (1976) developed an elastic method for getting judiciously resourceful resolvable designs for replication r, constant block size k and for a various values of v. They also reformed their methods with two different block sizes, k and k – 1 to find resolvable designs. As a practical point of view see John et al. (1999) when block sizes are unequal for resolvable designs. For instance, Patterson and Hunter (1983) had unequal block sizes about half of 245 experiments examined by them. See also Patterson and Silvey (1980), when block sizes need not be equal, the literature comprises of no organized work on defining optimal resolvable block designs. Morgan and Reck (2007) discussed the distinct situation of two blocks per replicate. In each replicate with only two blocks, necessarily a block be large in the sense of consisting at least half of the treatments. And with two blocks per replicate, the block sizes should not be equal for any odd v or not odd v.

The paramount of interest in this communication is to investigate new designs for complete diallel cross (CDC) design by using resolvable BIB design for some specific values of v, b and k. This paper is managed in this way like as. The method of resolvable design, CDC design and cyclic method of shifts are briefly described in section 2. How we obtain efficiency of designs also discuss here. In section 3, The method of cyclic shifts is explained through example to construct resolvable BIB designs, furthermore, these resolvable BIB designs used to construct new CDC designs alongwith MS-optimal criterion by Shah (1960), Eccleston and Hedayat (1974). The concluding remarks appear in Section 4.

Materials and Methods

Resolvable design

A block design is assumed to be resolvable if the blocks are alienated into replicates, described as sets of blocks with the condition that each treatment is assigned to one unit in each set. The realistic impact of, and motivation for, resolvability is to get orthogonality between concerned nuisance factors and treatments. Alternatively, a BIB design is called resolvable if the blocks of the BIB design can be partitioned into r groups such that each group contains each of the v treatments exactly once. Undoubtedly b/r = x, where x is the number of blocks in each resolvable group.

In a resolvable design the v = kx treatments are arranged in r resolvable groups (i.e. equal to no. of repliations) of x blocks and each block containing k plots. Within each group, each treatment is replicated one time. Resolvable blocks designs, are known as special type of the lattics designs, for selected restricted numbers of treatments and block sizes. Square lattices have k=x, whereas for rectangular lattices k = x-1.

The methods of shifts, which is introduced by Iqbal (1991) can also be used to obtain many resolvable designs. He also gives.

.....(1)

which shows each pair occur λ time. Clatworthy (1973) present a catalogue which shows the resolvability of group-divisible designs and other partially balanced incomplete block (PBIB) designs with two associate classes. However, above mentioned designs are generally lattic designs or less efficient alternatives.

Series 1 By Gupta and Kageyama (1994), “Let p is even, take D as p - 1 replications of the complete block in p treatments. Then there exists a resolvable balanced incomplete block design Dn with block size 2 and λn = 1 which is nested within D”.

Diallel cross design

In animal and plant procreation experiments, design of experiments for diallel crosses is taken under consideration to find the genetic properties of inbred lines. Srivastav and Shankar (2007) described the terminology and notation and the same was adopted in the present study. In the terminology and notation of them, think about a group of p parental lines(i.e. v treatments), and assume a diallel cross between parental lines i and i′ be denoted as i× i for i< i′ = 0, 1, 2, … , p-1. A diallel cross design is known as CDC if it takes each of the v′ = p(p-1)/2 distinct crosses. Griffing (1956) referred a CDC design as type IV mating design. Think about an arrangement of diallel crosses with p parental lines locate in b blocks, with each block containing k′ <v′ crosses such that:

• Each value of p occurs in exactly w crosses.
• Each value of p occurs less than or equal to one in any single block.
• Each cross occurs in exactly l blocks.
• Each pair of p occurs in exactly λ blocks, after ignoring crosses.
• These designs will be labeled as BIBDC(p, b′, w, k′, λ ,l) i.e. BIB design and refer to as BIBDCs. The necessary conditions for BIBDCs can easily be established as:

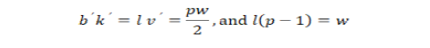
Efficiency of diallel cross design

Theorem 1 By Ghosh and Das (2003), Let 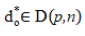be a diallel cross design, and assume 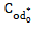satisfies

•
and
•
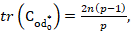
is completely symmetric in the sense that
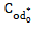has all its diagonal elements equal and all its off-diagonal elements equal.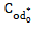

Where; n is crosses (in our paper total number of crosses is denoted by v′), p is parental line, 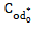for more detail see Ghosh and Das (2003). Then is A-optimal in D (p, n).

In another way, Shah (1960), Eccleston and Hedayat (1974) introduced the MS-optimal to locate families of efficient designs and optimal mating design.

Results and Discussion

Here, we consider the construction of CDC designs by resolvable BIB designs. New proposed designs given in Table 3.

Table 1: Replication for Resolvable Design.

Replicate	1		2		3
Block	1	3	2	4	5	6
	0	2	1	3	0	1
	1	3	2	0	2	3

Example 1

Construct resolvable balance incomplete block design by method of cyclic shifts

In Table 3 we gave the sets of shifts which used to construct resolvable BIB designs. Where the set of shifts developed by method of cyclic shift, which is introduced by Iqbal (1991). In the last column of Table 3, the index numbers of the blocks in each design which contain complete replicates are given by us. Consequently, for instance, construct resolvable BIB design consider first design of Table 3, then make a Table 1 as, Blocks 1 and 3 form a complete replicate and Blocks 2 and 4 form a complete replicate and Blocks 5 and 6 form a complete replicate. We use these resolvable BIB designs to construct CDC design.

v =4, k = 2, r = 3, b = 6, sets of shifts [1] + [2]1/2

Design 1

0	1	2	3	0	1
1	2	3	0	2	3

By using Equation (1)

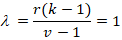
This design is BIB design because λ = 1, λ = 1 mean each treatment pair occurs one time.

Table 2: Replication for Resolvable Design.

Replicate	1		2		3		4		5		6		7
Block	1	11	2	12	3	13	4	14	5	8	6	9	7	10
	0	3	1	4	2	5	3	6	4	0	5	1	6	2
	1	5	2	6	3	0	4	1	5	2	6	3	0	4
	2	6	3	0	4	1	5	2	6	3	0	4	1	5
	4	7	5	7	6	7	0	7	1	7	2	7	3	7

Converting into resolvable balance incomplete block design

Index number of blocks which contain complete replicates (1,3), (2,4), (5,6).

This can be converted in Table 1 to form replicate like as Here index number of blocks (1,3), (2,4), (5,6) define as Block 1 and 3 make complete set, Block 2 and 4 make complete set and Block 5 and 6 make complete set.

Converting resolvable balance incomplete block design into complete diallel cross design

Now making all possible pair wise crosses within the treatment within each block. In the above design, there is 6 crosses, each cross replicated equal number of time say once, which are given below.

(0×1) (2×3) (1×2) (3×0) (0×2) (1×3)

It fulfill all the properties of CDC design which is described by Srivastav and Shankar (2007). This design is MS-optimal.

Table 3: Resolvable balanced incomplete block design and diallel cross design.

Parameters of Resolvable Balanced Incomplete Block Design							Parameters of Complete diallel cross design
V	k	R	b	x	Set of shifts	Index number of blocks which contain complete replicates	v/	k/	b/	λ
4	2	3	6	2	[1] + [2]1/2	(1,3), (2,4), (5,6)	6	1	6	1
6	2	5	15	3	[1]+[2]+ [3]1/2	(1,9,10),(3,11,12), (5,7,8), (2,4,6), (13,14,15)	15	1	15	1
6	3	10	20	2	[1,1]+ [1,2] + [3,2] + [2,2]1/3	(1,4),(2,5),(3,6),(7,18),(8,13),(9,14),…,(12,17),(19,20)	15	3	20	4
8	2	7	28	4	[1]+[2]+[3]+[4]1/2	(1,3,5,7),(2,4,6,8),(9,10,13,14),(11,12,15,16),(17,19,21,23), (18,20,22,24),(25,26,27,28)	28	1	28	1
8	4	7	14	2	[1,1,2]+[2,1]t	(1,11),(2,12),(3,13),(4,14),(5,8),(6,9),(7,10)	28	6	14	3
9	3	4	12	3	[1,2]+[4(1/2)]t	(1,5,11),(2,6,12),(3,7,9), (4,8,10)	36	3	12	1
10	2	9	45	5	[1]+[2]+[3]+[4]+ [5]1/2	(1,13,14,17,18),(2.25.26.37.40),(3,5,7,19,20),(4,27,28,32,39),(6,29,30,31,34,),(8,21,22,33,36),(9,11,12,15,16),(10,23,24,35,38), (41,42,…,45),	45	1	45	1
12	2	11	66	6	[1]+[2]+[3]+[4]+ [5]+[6]1/2	(1,3,41,…,44),(2,52,…,56),(4,6,10,12,51,57),(5,11,39,40,45,46),(7,9,37,38,47,48),(8,49,50,58,59,60),(13,14,17,18,21,22),(15,16,19,20,23,24),(25,26,27,31,32,33), (28,29,30,34,35,36), (61,…,66)	66	1	66	1
12	3	11	44	4	[1,1]+[3,3]+[4,4]+ [5,5]2/3	(1,4,7,10),(2,5,8,11),(3,6,9,12),(13,17,21,38),(14,18,22,39),(15,19,23,40),(16,20,24,37),(25,29,33,44),(26,30,34,41),(27,31,35,42),(28,32,36,43)	66	3	44	2
12	4	11	33	3	[1,2,4] + [1,2,5] + [1,2]t	(1,14,28),(2,15,29),…,(6,19,33),(7,20,23),(8,21,24),(9,22,25),(10,12,26),(11,13,27)	66	6	33	3
12	6	11	22	2	[1,1,2,1,2]+ [3,2,1,1,]t	(1,15),(2,16),…,(8,22),(9,12),(10,13),(11,14)	66	15	22	5
14	2	13	91	7	[1]+[2]+[3]+[4]+ [5]+[6]+[7]1/2	(1.6.9.36.68.69.70),(2.7.23.24.83.84),(3,5,11,21,22,27,28),(4,8,10,12,14,44,45),(13,71,…,76),(15,30,37,46,52,62,77),(16,31,38,47,53,63,78),(17,32,39,48,54,64,79),(18,33,40,49,55,65,80),(19,34,41,50,56,66,81),(20,355,42,43,51,67,82),(25,26,57,…,61),(85,…,91),	91	1	91	1
15	3	7	35	5	[1,3]+[2,6]+ [5,5]1/3	(1,6,11,33,34),(2,22,23,26,27),(3,5,10,12,30),(4,24,25,28,29),(7,13,16,19,35),(8,14,17,20,31),(9,15,18,21,32)	105	3	35	1
16	2	15	120	8	[1]+[2]+[3]+[4]+ [5]+[6]+[7]+ [8]1/2	(1,3,…,15),(2,4,…,16),(17,18,23,24,27,28,95,96),(19,20,87,…,92),(29,30,81,…86),(33,34,48,70,…,74),(21,22,25,26,31,32,93,94),(35,36,40,41,42,46,47,80),(37,38,39,75,…79),(43,44,45,65,…69),(49,…,52,57,…60),(53,…,56,61,…164),(97,99,…,111),(98,100,…,112),(113,…,120).	120	1	120	1
16	4	5	20	4	[1,2,4]+{[55]1/3}t	(1,6,11,20),(2,7,12,16),(3,8,13,17),(4,9,14,18),(5,10,15,19).	120	6	20	1
16	8	15	30	2	[1,1,1,2,2,1,3]+ [2,3,1,2,1,1]t	(1,20),(2,21),…(11,30),(12,16),(13,17),…,(15,19)	120	28	30	7
18	2	17	153	9	[1]+[2]+[3]+[4]+ [5]+[6]+[7]+[8] +[9]1/2	(1,13,26,27,123,…,126,147),(2,4,…,18),(7,135,…,142),(17,127,…,134),(22,23,116,…,122),(19,20,28,29,149,…,153),(24,25,30,31,88,89,90,145,146),(33,34,109,…,115),(37,38,39,97,…,102),( 40,41,42,46,47,48,52,53,54),(43,44,45,403,…,108),(49,50,51,91,…,96),(55,70,71,72,78,…,82),(57,…,60,83,…,87),(65,…,68,73,…,77)	153	1	153	1

Example 2

Construct resolvable balance incomplete block design by method of cyclic shifts

The established two set of shifts for v=8, k=4, r=7, b=14, used to construct the original design for v=8, k1=4 and k2=3, is [1,1,2] and [2,1] given in Table 3. This explain as that the blocks of size 4 are obtained by combining the blocks obtained using shift [1,1,2,2], [2,1] t. We note that for [2,1]t, treatment 7 has been added to each block of the smaller design according Iqbal (1991).

Design 2

0	1	2	3	4	5	6	0	1	2	3	4	5	6
1	2	3	4	5	6	0	2	3	4	5	6	0	1
2	3	4	5	6	0	1	3	4	5	6	0	1	2
4	5	6	0	1	2	3	7	7	7	7	7	7	7

Converting into resolvable balance incomplete block design

Index number of blocks which contain complete replicates (1,11), (2,12), (3,13), (4,14), (5,8), (6,9), (7,10) This can be converted in Table 2 to form replicate like as.

Converting resolvable balance incomplete block design into complete diallel cross design

Now making distinct crosses in each block according to our scheme, we get ½ k(k-1)=6 crosses in each block. Thus, we get ½bk (k-1= 84 arranged in b=14 blocks. Now we get CDC design with parameters v/= ½ p (p-1=28, b/=b, k/ = ½ k(k-1).

Blocks	Treatments (Crosses)
1	0×1	0×2	0×4	1×2	1×4	2×4
2	1×2	1×3	1×5	2×3	2×5	3×5
3	2×3	2×4	2×6	3×4	3×6	4×6
4	3×4	3×5	3×0	4×5	4×0	5×0
5	4×5	4×6	4×1	5×6	5×1	6×1
6	5×6	5×0	5×2	6×0	6×2	0×2
7	6×0	6×1	6×3	0×1	0×3	1×3
8	0×2	0×3	0×7	2×3	2×7	3×7
9	1×3	1×4	1×7	3×4	3×7	4×7
10	2×4	2×5	2×7	4×5	4×7	5×7
11	3×5	3×6	3×7	5×6	5×7	6×7
12	4×6	4×0	4×7	6×0	6×7	0×7
13	5×0	5×1	5×7	0×1	0×7	1×7
14	6×1	6×2	6×7	1×2	1×7	2×7

It fulfill all the properties of CDC design which is described by Srivastav and Shankar (2007). This design is MS-optimal also.

Conclusions and Recommendations

Srivastav and Shankar (2007) described the terminology and notation of diallel cross design. Yalew and Sharma (2010) used the same terminology for the construction and analysis of complete diallel cross. A complete diallel cross design referred as type IV mating design by Griffing (1956). In this paper, we proposed new methods for the construction of diallel cross design which is known as method of cyclic shifts.

The current study concluded that we constructed the auxiliary design for diverse set of treatment v and block size k through method of cyclic shifts, after that we obtained resolvable BIB design and finally these resolvable BIB design used to construct complete diallel cross design which fulfil the properties of CDC design. After that, we also checked that these diallel cross designs are MS-optimal.

The important aspect of the method of cyclic shifts is that the properties of a design can be obtained from the off-diagonal elements of the concurrences matrix without constructing the actual blocks of the design.

To come across the detail that how the technique of cyclic shifts is of use for developing other experimental designs, the researcher may refer to Iqbal and Tahir (2009).

Author’s Contribution

Ijaz Iqbal: Generated the idrea of the study.

Maqsooda Parveen: Developed the methodology and wrote the manuscript.

Zafar Mahmood: Proffread the final manuscript.

References

Abel, R.J.R., G. Ge, M. Greig and L. Zhu. 2001. Resolvable balanced incomplete block designs with block size 5,” J. Stat. Plan. Inference. 95: 49- 65. https://doi.org/10.1016/S0378-3758(00)00277-9

Antoine, B., B.B. Joseph, T. Jean-Baptiste, D. Zakaria, S. Hamadou and S. Mahamadou. 2017. Diallel analysis of cowpea populations for resistance to Cowpea aphid-born mosaic virus disease (CABMV) in Burkina Faso. J. Plant. Breed. Crop Sci. 9(7): 90-97. https://doi.org/10.5897/JPBCS2016.0628

Bailey, R.A., H. Monod and J.P. Morgan. 1995. Construction and optimality of affine resolvable designs, Biometrika. 82(1): 187-200. https://doi.org/10.1093/biomet/82.1.187

Clatworthy, W.H. 1973. Tables of two-associate-class partially balanced design. Nat. Bureau of stand. (U.S.), Appl. Math. Series. 63.

Craigen, R. and H. Kharaghani. 2007. Hadamard matrices and hadamard designs. In handbook of combinatorial designs, 2nd ed. (C.J. Colbourn and J.H. Dinitz, eds.) 2007, 273–280. Chapman and Hall/CRC, Boca Raton, FL,

Das, A., A. Dey and A.M. Dean. 1998. Optimal designs for diallel cross experiments, Stat. Probabil. Lett. 36: 427-436.

Dey, A. and C.K. Midha. 1996. Optimal designs for diallel crosses, Biometrika, 83(2): 484-489. https://doi.org/10.1093/biomet/83.2.484