Introduction
After maize in terms of production, wheat is the cereal grain with the second-highest global trade volume. It is the main crop and is regarded as the king of all cereal crops due to its ease of production, ecological suitability and great nutritional value. It is particularly rich in proteins (7–22%), carbohydrates, calcium, lysin, iron, gluten, vitamin D, and minerals (Abdel-Lateif and Hewedy, 2018). The wheat crop prefers a temperate climate for growth and is primarily consumed in tropical and subtropical regions of the world (Sharma et al., 2019). The total amount of wheat produced worldwide in 2020 was 760 million tons. China, India, and Russia are the top three individual wheat producers in the world, producing 136.95, 109.52, and 75.5 million metric tons of wheat respectively, moreover accounting for about 41% of the total amount of wheat produced worldwide. Pakistan comes at seventh number in wheat production of 27 million metric tons. During the Green Revolution, the expansion of irrigation, heavy use of fertilizers, and improved breeding techniques all contributed to a nearly three-fold increase in the global average yield (Ahmad et al., 2013). However, production of wheat is currently less than its potential with the average global yield being only 3 tons per hectare (Ahmad et al., 2014). Wheat yield needs to be increased by more than 60% in maintaining or improving its nutritional qualities to feed the estimated 9 billion people by the year 2050 (Ahmad et al., 2014). The emphasis must be placed on critical features related to plant productivity and response to environmental difficulties in order to accomplish this aim without increasing the area of cultivated land, which is simply not possible. The shortage of this important staple crop could pose a significant threat to the global food security. High grain production is the main goal of most wheat breeding initiatives; hence it is required to use a variety of better breeding approaches to break through the current yield limit (Ahmad et al., 2013).
Triticum aestivum is a hexaploid species, but Triticum durum is just a tetraploid and is more extensively cultivated. Wheat is a member of the poaceae family. In addition, only a small amount of the other two varieties of wheat, such as the diploid and hexaploid Triticum monococcum and Triticum spelta, are grown In order to choose genetically distant parents for hybridization, numerous research on the genetic variability of various crop species based on quantitative and qualitative features have been carried out (Akel et al., 2018). The most practical and environmentally benign method to sustainably enhance wheat output is genetic improvement to create varieties with high yield potential, resistance/tolerance to biotic and abiotic stressors, and acceptable end-use quality. Such crop improvement necessitates the creation and introduction of genetic variation, inbreeding combined with selection, extensive evaluation of breeding materials at various locations to identify stable genotypes with desired agronomic traits, and inbreeding alone or in combination with selection. Therefore, such knowledge is crucial for the development of genetic variation and ongoing bread wheat improvement generally in the nation (Reddy et al., 2012).
Breeders can exclude less productive crossings throughout the early generation by studying heterosis. The breeder would be able to concentrate on a smaller number of potentially more fruitful crosses by rejecting crosses that do not exhibit heterosis. The exploitation, application, and viability of hybrid seed development determine the degree of heterosis in a crop. In a crop like wheat, heterosis could not be beneficial unless it can be used to create a hybrid. In wheat, attractive crossings are chosen in order to produce superior offspring in earlier generations, enriching the grain yield even further.
A decline in fitness and vigour brought on by inbreeding is referred to as inbreeding depression. A thorough selection of parents and populations that can produce offspring with desired trait combinations improves breeding programme efficiency The percentage of an increase or reduction in the mean value of the F1 hybrids above the value of their middle parents is known as heterosis. While heterosis is the percentage increase or reduction in the F1 hybrid’s mean value over its superior parent. A genetic manifestation of the advantageous effects of hybridization may be heterosis. To advance hybrid breeding in the future and improve the relevance of general combining ability (GCA) in comparison to specific combing capacity, however, the identification or production of heterotic groups represents a significant challenge (EL Saadoown et al., 2017). The most crucial steps in the production of novel varieties that are superior in terms of yield and quality features in combination breeding are the choice of parents and the identification of suitable hybrid combinations. Heterosis is the phenomenon in which the offspring of two genetically dissimilar individuals outperforms either the average of the parents or the superior parent (heterobeltiosis). Fiber, cereal, and oilseed crops have all effectively used this phenomenon (Ali, 2019).
It can be suggested to use the crossings showing the best heterosis and heterobeltiosis to enhance the corresponding features. The Plant breeders can acquire estimates of general combining ability (GCA) and particular combining ability using half diallel design, a sort of mating system (SCA) (Charity Aremu, 2012). In order to get around plant breeding programmes that claim the combining ability is the most reliable biometrical method (Aljanaby, 2019). Diallel mating design has been widely utilised to find the best specific crossings for yield and various quality metrics as well as parents with superior potential to pass on desirable traits to their offspring. Understanding the genetic foundation of yield, its contributing features, general combining ability (GCA), special combining ability (SCA), and the function of genes in the breeding material is crucial for an efficient breeding programme. The combining ability analysis is a useful technique for this goal since it can distinguish between good and bad combiners to choose the best parental materials for the desired traits in the wheat improvement programme (Ayoob, 2020). Grain yield is mostly based on the increase and improvement of yield components, such as plant height, the number of grains and grain weight per spike in wheat, the productive stems per unit area, and spike length. All of these yield components are genetically predetermined and diallel crosses of (Triticum aestivum L) can demonstrate the genetic control of yield components. The genotypes of the parents employed for diallel crossing have a significant influence on this kind of inheritance and the impact of genes. Due to this, it is necessary to choose the right wheat parental cultivars for the breeding programme (Birchler et al., 2003). Reduced genetic diversity makes crops more susceptible to diseases and harmful weather changes (Budak, 2001).
One of the traditional methods used in biometrical genetics to get sufficient data regarding the inheritance of a quantitative feature is the diallel cross technique. In order to estimate the amount of genetic diversity attributable to variations between the parental lines, the method first proposed by Schmidt in 1919 includes crossing a set of parental lines in every feasible combination, including their reciprocals (Nirdesh, 2022).
Diallel analysis, as created by offers a methodical approach for describing parents and crosses that are superior for the traits being studied. It also aids plant breeders in selecting the most efficient method of selection for isolating superior genotypes among the hybrid progenies being studied. This has enabled plant breeders to compare heterotic patterns at an early stage of hybrid creation and develop the appropriate selection techniques (Hailegiorgis et al., 2011). The diallel analysis method has been used frequently for parent selection as a suitable strategy to quickly gather genetic information on yield traits that may be used to increase the effectiveness of wheat breeding programmes (Dave et al., 2021). A diallel cross between chosen parents can reveal details about the genetic variations in a population created by mating these parents at random. According to Ahmad et al., the diallel analysis is one of the breeding strategies for evaluating the combined influence of genotype ability and also provides details about the genetic mechanisms governing numerous features. Dave et al. (2021) further distinguished between these two types of combining ability (SCA). The phenomena of the capacity for combination have been explained by numerous geneticists.
Diallel crosses can be used to gather the whole genetic information on the variability of quantitative features in wheat cultivars (Dreisigacker et al., 2005). The majority of these research showed that the GCA effect, a measurement of additive genetic variation, was connected to a significant portion of the overall genetic variability for yield and its components. Plant breeders that work with autogamous crops frequently collect genetic data from diallel cross progenies. Every plant breeding programme must start with insight knowledge regarding the ideal parental mix, focused on a high degree of heterotic response (El-Gammaal and Yahya, 2018). The capacity to combine information also helps geneticists understand the behaviour of the genes responsible for the sign of measurable traits with profitable predominance. In the same way, diallel analysis is the most actual ways for similar to the GCA and SCA influence of parents and crosses separately (El-Gammaal and Yahya, 2018).
The success of a breeding programme depends mainly upon the amount of genetic variation present in the population and the extent to which the desired qualities are heritable (Francis et al., 1969). The Balochistan province with a food insecurity problem, consumes 150 kg of wheat per person yearly and needs 1.85 million tonnes of wheat to sustain its 1.23 million residents. According to Pakistan’s economic survey for 2020–21, wheat was grown in Balochistan on 458.006 thousand acres, yielding 1.16 million tonnes. However, compared to the other provinces in the nation, the province’s average yield is too low. The creation of novel, high-yielding wheat varieties that are tolerant of changing climates is essential for increasing output per unit area and enhancing average yield vertically. Given the significance of the combining ability effect, the nature of gene actions in regulating the expression of quantitatively inherited traits and heterosis in wheat breeding programmes, the current study used F1 diallel cross combinations and their parents to focus on the following broad objectives.
Materials and Methods
Genetic material for research were comprised of six wheat genotypes and there F1were sown in field area of Agriculture Research Institute, Sariab, Quetta. During Rabi season 2017-2018 successfully crossed the genotypes in 6 x 6 half diallel fashion to yield 15 F1 crosses, excluding reciprocal crosses.
Selection of genotypes on the basis of following characteristics
Zardana: High yielding, best adopted in all agro-climatic condition of Balochistan and good baking quality.
Umeed: High yielding, lodging resistance, top ranker in Zinc more than 50 ppm and 3rd ranker in Iron 52 ppm (Analyzed at HEJ institute and WRI Lab. Faisalabad report in comparison with top ten wheat varieties of Pakistan).
Raskoo: Good in yield, drought tolerant, good baking quality, MSMR type of rust reaction (horizontal resistance i.e., controls by minor genes).
TD1: (ARI/Tandojam): It is a good yield promising variety. Short stature, good responsive to N fertilizer and salt tolerant.
Benazir: (WRI Sakrand): high yielding, disease resistance.
Hamal: Semi dwarf Rht gene carrier and good responsive in mega environment.
Germination percentage GP (%)
Germination percentage was calculated by using the equation:

Objective for each cross
|
Crosses |
Objective |
|
TD1 x Zardana |
To develop genetic diversity for high yield, salinity tolerance, and fertilizer responsiveness |
|
TD1 x Umeed |
Increasing salinity tolerance and genetic variability for yield height |
|
TD1 x Raskoo |
To create genetic variability for high yield, salinity tolerance |
|
Benazir x Zardana |
To create genetic variability for yield, and disease resistance in Zardana |
|
Benazir x Umeed |
To create genetic variability for yield, and disease resistance |
|
Benazir x Raskoo |
In order to produce genetic diversity for yield and disease resistance |
|
Hamal x Zardana |
To create genetic variability for yield height, good baking quality in every environment |
|
Hamal x Umeed |
To create genetic variability for lodging resistance, top zinc ranker, no damage by bird |
|
Hamal x Raskoo |
To create genetic variability for high yielding, drought tolerant and good baking quality in mega environment |
Days to maturity (75%)
Data was calculated of days to maturity at various dates.
Plant height (cm)
Homogeneous plants were opted for plant height and measurement were taken from the base to the top. For plant height average plant was estimated.
Number of tillers plant-1
The plant from each row of parents and F1 were selected randomly before maturity and count individually.
Harvest index (%)
After threshing, the selected genotypes Harvest index (HI) was calculated. The average biological yield per plant was multiplied by 100 and the average seed weight per plant was split accordingly.
The harvest index was calculated using the formula below:
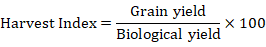
Spike density
After threshing spikes of randomly selected plants, spike density was calculated. For this purpose, number of spikelets per spike was divided with spike length.
The formula below was used to calculate the spike density.

Spikelets spike-1
Counting Spikelets per spike were done on the spike of each guarded plant in a row. Non fertilespikelets on the lower portion of the spike were counted and the average data was estimated.
Fresh weight (g)
Weight of selected plant along with stem, flag leaf, peduncle, spike as well as root were weighted with electronic balance in grams for data recording.
Dry weight(g)
At physiological maturity, weight of selected plant along with stem, flag leaf, peduncle, spike as well as root were weighted with electronic balance in grams for data recording.
Flag leaf area (cm2)
Flag leaf area were recorded by measuring the length and width of flag leaves from 10 randomly selected tillers in each plot at anthesis stage and were averaged, then the average leaf area was recorded by the formula.
Leaf area = leaf length x width x 0.75 (Francis et al., 1969)
Where; 0.75 is the correction factor for leaf area.
Number of grain spike-1
Using a single head thresher machine, the spikes of the same genotypes were threshed after reaching physiological maturity in order to count the total amount of grains per spike. At the conclusion, average counts of grains per spike for each plant were reported.
Thousand grain weight (g)
Thousand grains weight was recorded by the application of an electronic balance (Compax, RS232C)s. For this purpose, grains of 1000 seeds from the final product of each plant were counted by the machine known as seed counter and then weighed with the help of an electronic balance.
Grains yield plant-1(g)
A single selected plant threshed after physiological maturity by utilization of the electronic balance. And all grains were weighted with the help of electronic balance.
Yield per hectare (kg)
First of all, seed of one meter per square were harvested, and weighted its weight. Where, per acre yield were estimated by multiplication with its per meter production. At last, yield of one acre multiplied with 2.47 for per Hector production.
Statistical analysis
The recorded information was subjected to statistical analysis in order to elaborate the results. The methods of ANOVA and correlation were followed for appropriate and systematic breakdown of findings of the research. Fisher’s analysis of variance method at 5% probability level was used to check the variance among treatment means (Steel et al.,1997) for GCA and SCA method model l method 2 was used and heterosis was determine according to Fehr (1987).
Heterosis
The heterosis of F1s of mid parent and the better parent was calculated by following formula given by (Geleta et al., 2004).
Heterosis over mid-parent values
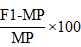
Heterosis over better parent
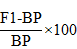
Were; MP = Mid-parent value (Average value of the two parents involved in a specific cross). BP = Better parent value (Value of the better of the two parents in a cross combination).
Heterosis values were statistically tested for significance using the student t-test (Sousa and Maluf, 2003).
Results and Discussion
Analysis of variance (ANOVA)
The analysis of variance (ANOVA) for germination percentage is shown in Table 1. From the Table 1 it can be figured out that blocks were non-significant meaning that block were inefficient in reducing the experimental error. However, the genotypes were highly significant meaning that at least 2 genotypes were significantly different from one another and there is variation present in the genotypes to further exploit it for future experimental procedures.
Table 1: Analysis of variance for germination percentage %.
|
Source of variation |
Degree of freedom |
Sum of square |
Mean sum of square |
F |
|
Block |
2 |
1.35 |
0.68NS |
1.74 |
|
Genotype |
20 |
89.69 |
4.48** |
11.49 |
|
Error |
40 |
15.52 |
0.39 |
|
|
Total |
62 |
106.56 |
*=significant (p<0.05), **=high significant (p<0.01), NS= non-significant (p>0.05).
Days to maturity (75%)
The ANOVA result regarding days to physiological maturity is presented in (Table 2). The ANOVA table determines that the blocks showed a positively significant while genotypes remained highly significant.
Table 2: Analysis of variance for days to maturity.
|
Source of variation |
Degree of freedom |
Sum of square |
Mean sum of square |
F |
|
Block |
2 |
5.2 |
2.6* |
5.2 |
|
Genotype |
20 |
337.1 |
16.86** |
33.72 |
|
Error |
40 |
20.13 |
0.5 |
|
|
Total |
62 |
362.44 |
*=significant (p<0.05), **=high significant (p<0.01), NS=non-significant (p>0.05).
Plant height (cm)
The significant variation was found in all genotypes about plant height. The blocks remained non-significant result as shown in (Table 3).
Number of tillers per plant
The analysis of variance stated that the genotypes showed statistically significant variation regarding number of tillers. While the blocks remained non-significant (Table 4).
Table 3: Analysis of variance for plant height (cm).
|
Source of variation |
Degree of freedom |
Sum of square |
Mean sum of square |
F |
|
Block |
2 |
1.36 |
0.68NS |
0.41 |
|
Genotype |
20 |
3122.8 |
156.14** |
94.63 |
|
Error |
40 |
66.12 |
1.65 |
|
|
Total |
62 |
3190.28 |
*= significant (p<0.05), **= high significant (p<0.01), NS= non-significant (p>0.05).
Table 4: Analysis of variance for number of tillers.
|
Source of variation |
Degree of freedom |
Sum of square |
Mean sum of square |
F |
|
Block |
2 |
4.98 |
2.49NS |
2.39 |
|
Genotype |
20 |
3878.6 |
193.93** |
186.5 |
|
Error |
40 |
41.68 |
1.04 |
|
|
Total |
62 |
3925.27 |
Table 5: Analysis of variance for harvest index.
|
Source of variation |
Degree of freedom |
Sum of square |
Mean sum of square |
F |
|
Block |
2 |
1.16 |
0.58NS |
0.73 |
|
Genotype |
20 |
10567.45 |
528.37** |
668.8 |
|
Error |
40 |
31.8 |
0.79 |
|
|
Total |
62 |
10600.41 |
*=significant (p<0.05), **=high significant (p<0.01), NS=non-significant (p>0.05).
Harvest index (%)
The ANOVA result regarding harvest index determined that the genotypes showed significant variation while block remained non-significant as shown in (Table 5).
Spike density
The ANOVA about spike density is presented in (Table 6). The genotypes showed significant variation while blocks remained non-significant.
Table 6: Analysis of variance for spike density.
|
Source of variation |
Degree of freedom |
Sum of square |
Mean sum of square |
F |
|
Block |
2 |
0.014 |
0.007NS |
0.538 |
|
Genotype |
20 |
9.77 |
0.489** |
37.62 |
|
Error |
40 |
0.533 |
0.013 |
|
|
Total |
62 |
10.317 |
*=significant (p<0.05), **= high significant (p<0.01), NS= non-significant (p>0.05).
The ANOVA results about spikelet per spikes presented in (Table 7). From table, it is clearly determined that the genotypes were significantly different from each other. On the other hand, the blocks remained non-significant.
Table 7: Analysis of variance for spikelet spike-1.
|
Source of variation |
Degree of freedom |
Sum of square |
Mean sum of square |
F |
|
Block |
2 |
1.52 |
0.76NS |
0.7 |
|
Genotype |
20 |
419.52 |
20.98** |
19.07 |
|
Error |
40 |
43.81 |
1.1 |
|
|
Total |
62 |
464.86 |
Fresh weight (g)
The ANOVA result regarding fresh weight determined that the genotypes showed significant variation while block remained non-significant as shown in (Table 8).
Table 8: Analysis of variance for fresh weight.
|
Source of variation |
Degree of freedom |
Sum of square |
Mean sum of square |
F |
|
Block |
2 |
11.87 |
5.94NS |
1.63 |
|
Genotype |
20 |
9213.78 |
460.69** |
126.564 |
|
Error |
40 |
145.63 |
3.64 |
|
|
Total |
62 |
9371.28 |
*=significant (p<0.05), **= high significant (p<0.01), NS= non-significant (p>0.05).
Dry weight (g)
The ANOVA results pertaining dry weight is presented in Table 9. From table, it is clearly determined that the genotypes were significantly different from each other. On the other hand, the blocks remained non-significant.
Table 9: Analysis of variance for dry weight.
|
Source of variation |
Degree of freedom |
Sum of square |
Mean sum of square |
F |
|
Block |
2 |
0.22 |
0.11NS |
0.16 |
|
Genotype |
20 |
418.98 |
20.95** |
30.91 |
|
Error |
40 |
27.11 |
0.68 |
|
|
Total |
62 |
446.32 |
Flag leaf area (cm2)
Flag leaf area has a direct relationship with grain yield. the ANOVA results shows that the block was non-significant. The genotypes showed a statistically significant variation as shown in table (Table 10).
Table 10: Analysis of variance for flag leaf area.
|
Source of variation |
Degree of freedom |
Sum of square |
Mean sum of square |
F |
|
Block |
2 |
1.81 |
0.91NS |
0.9 |
|
Genotype |
20 |
4759.43 |
237.97** |
236.85 |
|
Error |
40 |
40.19 |
1 |
|
|
Total |
62 |
4801.43 |
Number of grains spike-1
The ANOVA results pertaining number of grains spike-1 is presented in (Table 11). From table, it is clearly determined that the genotypes were significantly different from each other. On the other hand, the blocks remained non-significant.
Table 11: Analysis of variance for number of grains spike-1.
|
Source of variation |
Degree of freedom |
Sum of square |
Mean sum of square |
F |
|
Block |
2 |
183.85 |
91.92NS |
1.73 |
|
Genotype |
20 |
2321.75 |
116.09* |
2.18 |
|
Error |
40 |
2126.15 |
53.15 |
|
|
Total |
62 |
4631.75 |
Grain yield (g)
Grain yield and its quality are the principal characters of a cereal crop. They are complex quantitative characters, which are influenced by yield contributing characters. Hence, the selection for desirable genotypes should not only be based on yield alone, and the other yield components should also be considered. The ANOVA result for grain yield is presented in (Table 12). The highly significant variation found in genotypes. Whereas the block remains non-significant.
Table 12: Analysis of variance for grain yield.
|
Source of variation |
Degree of freedom |
Sum of square |
Mean sum of square |
F |
|
Block |
2 |
22.86 |
11.43NS |
1.57 |
|
Genotype |
20 |
5035.74 |
251.79** |
34.5 |
|
Error |
40 |
291.89 |
7.3 |
|
|
Total |
62 |
5350.49 |
*=significant (p<0.05), **= high significant (p<0.01), NS= non-significant (p>0.05).
Conclusions and Recommendations
The study was designed to estimate heterosis, general combining ability and specific combining ability in bread wheat. For development of heterotic population, it is important to exploit specific combining ability for dominant gene asction by crossing indigenous genotypes with exotic germplasm with improved rust resistance, which will be a useful future breeding strategy.
Novelty Statement
For development of yield related traits, six wheat genotypes were sown for crossed of the genotypes in 6 x 6 half diallel to yield 15 F1 crosses to get more cultivar and hybrids.
Author’s Contribution
Muhammad Ayyub: Conducted the research, analysis and wrote the MS.
Mitha Khan, Syed Abdul Malik and Sakhawat Ali: Helped in data collection.
Syed Shamsullah, Mujeeb ur Rehman, Ikhlaq Ahmed and Ameer Uddin: Helped in data analysis.
Habibullah Kakar, M Zahid, Khalil Ahmed, Mana Khan and Mukhtiar Ahmed: Helped in relevant literature.
M. Rafiq Khetran, Zia ul Haq and M. Azam: Helped in proofreading and format setting.
Conflict of interest
The authors have declared no conflict of interest.
References
Abdel-Lateif, Khalid and O. Hewedy. 2018. Genetic diversity among egyptian wheat cultivars using SCoT and ISSR markers. Sabrao J. Breed. Genet., 50: 36-45.
Ahmad, M., M. Iqbal, A. Shahzad, M. Asif and M. Sajad. 2013. Genetic analysis of yield and yield contributing quantitative traits in bread wheat under sodium chloride salinity. J. Agric. Sci., 5: 10.5539/jas.v5n6p156. https://doi.org/10.5539/jas.v5n6p156
Ahmad, M.F., S. Shehzad, K. Hussain, S.H. Khan and M. Sajjad. 2014. Influence of Fusarium moniliforme inoculation on heterosis and heterobeltiosis for agronomic traits in maize (Zea mays). Int. J. Agric. Biol., 16; 1041-1049.
Ahmad, N.H., G. Shabbir, Z. Akram and M.K.N. Shah. 2013. Combining ability effects of some phenological traits in bread wheat. Sarhad J. Agric., 29(1): 15-20.
Akel, W., P. Thorwarth, V. Mirdita, E. Weissman, G. Liu, T. Würschum and C.F. Longin. 2018. Can spelt wheat be used as heterotic group for hybrid wheat breeding? Theor. Appl. Genet., 131: 973-984. https://doi.org/10.1007/s00122-018-3052-3
Ali, M., 2019. Combining ability of physiological and yield traits of bread wheat diallel crosses under timely and late sowing dates. Egypt. J. Agron., 41(2): 159-181. https://doi.org/10.21608/agro.2019.15182.1172
Aljanaby, A., 2019. Genetic diversity among bread wheat genotypes using RAPD and SSR markers. SABRAO J. Breed. Genet., 51: 325-339.
Ayoob, H.M., 2020. Combining ability analysis, estimation of heterosis and some genetic parameters using half diallel cross in bread wheat (Triticum aestivum L.). J. Educ. Sci., 29(1): 93-106. https://doi.org/10.33899/edusj.2020.164365
Birchler, J., A. Donald and N. Riddle. 2003. In search of the molecular basis of heterosis. Plant Cell, 15(10): 2236–2239. https://doi.org/10.1105/tpc.151030
Budak, N., 2001. Heterosis and combining ability in a 8 X 8 diallel durum wheat population. Ege Univ. Ziraat Fak. Dergisi, 38(2-3): 55-62.
Charity Aremu, 2012. Exploring statistical tools in measuring genetic diversity for crop improvement. chapters, Mahmut Caliskan (Ed.), Genetic Diversity in Plants, Intech Open. pp. 340-348.
Dave, M., A. Dashora, S.V. Saiprasad, D. Ambati, P. Malviiya, C. Urmila, N. Yadav and M. Anshul. 2021. Genetic variability, heritability and genetic advance in durum wheat (Triticum durum Desf.) genotypes. Pharm. Innov., 10(9): 221-224.
Dreisigacker, S., A.E. Melchinger, P. Zhang, K.Ammar, C. Flachenecker, H. David and W. Marilyn. 2005. Hybrid performance and heterosis in spring bread wheat, and their relations to SSR-based genetic distances and coefficients of parentage. Euphytica, 144: 51–59. https://doi.org/10.1007/s10681-005-4053-2
EL Saadoown, A.W., A.A. EL Hosary, S.A. Sedhom., M.EL.M. ELBadawy and A.A.A. El Hosary. 2017. Genetic analysis of diallel crosses in wheat under stress and normal irrigation treatments. Egypt. J. Plant Breed., 21(5): 279-292.
El-Gammaal, A.A., and A.B. Yahya. 2018. Genetic variability and heterosis in F1 and F2 generations of diallel crosses among seven wheat genotypes. J. Plant Prod., 9(2): 1075-1086. https://doi.org/10.21608/jpp.2018.36631
Fehr, W.R., 1987. Principles of cultivar development. Vol.1 Theory and Technique. Macmillan, New York.
Francis, C.A., J.N. Rutger and A.F. Palmer. 1969. A rapid method for plant leaf area estimation in maize (Zea mays L.). Crop Sci., 9: 537-539. https://doi.org/10.2135/cropsci1969.0011183X000900050005x
Geleta, L.F., M.T. Labuschagne and C.D. Viljoen. 2004. Relationship between heterosis and genetic distance based on morphological traits and AFLP markers in pepper. Plant Breed., 123(5): 467-473. https://doi.org/10.1111/j.1439-0523.2004.01017.x
Hailegiorgis, D., M. Mesfin and G. Tsige. 2011. Genetic divergence analysis on some bread wheat genotypes grown in Ethiopia. J. Central Eur. Agric., 12 (2): 344-352. https://doi.org/10.5513/JCEA01/12.2.922
Nirdesh, K.C., L.K. Gangwar, C. Pooran, S.K. Singh, K. Mukesh, M. Shiva and K. Pushpanjali. 2022. Analysis of combining ability for yield and its contributing traits in bread wheat (Triticum aestivum L.). Pharma Innov. J., 11(5): 2500-2504.
Reddy, M., H. Kadiyala, G. Mutyala and B. Hameedunnisa. 2012. Heterosis for yield and yield components in okra (Abelmoschus esculentus (L.) Moench). Chilean J. Agric. Res., 72: 316-325. https://doi.org/10.4067/S0718-58392012000300003
Sharma, A., V. Kumar, B. Shahzad and M. Tanveer. 2019. Worldwide pesticide usage and its impacts on ecosystem. SN Appl. Sci., 1: 1446. https://doi.org/10.1007/s42452-019-1485-1
Sousa, de J.A. and W.R. Maluf. 2003. Diallel analyzes and estimation of genetic parameters of hot pepper (Capsicum chinense Jacq.). Sci. Agricola, 60(1): 105-113. https://doi.org/10.1590/S0103-90162003000100016
Steel, R.G.D., J.H. Torrie and D.A. Dicky. 1997. Principles and procedures of statistics, A biometrical approach. 3rd Ed., McGraw Hill, Inc. Book Co., New York, pp. 352-358.